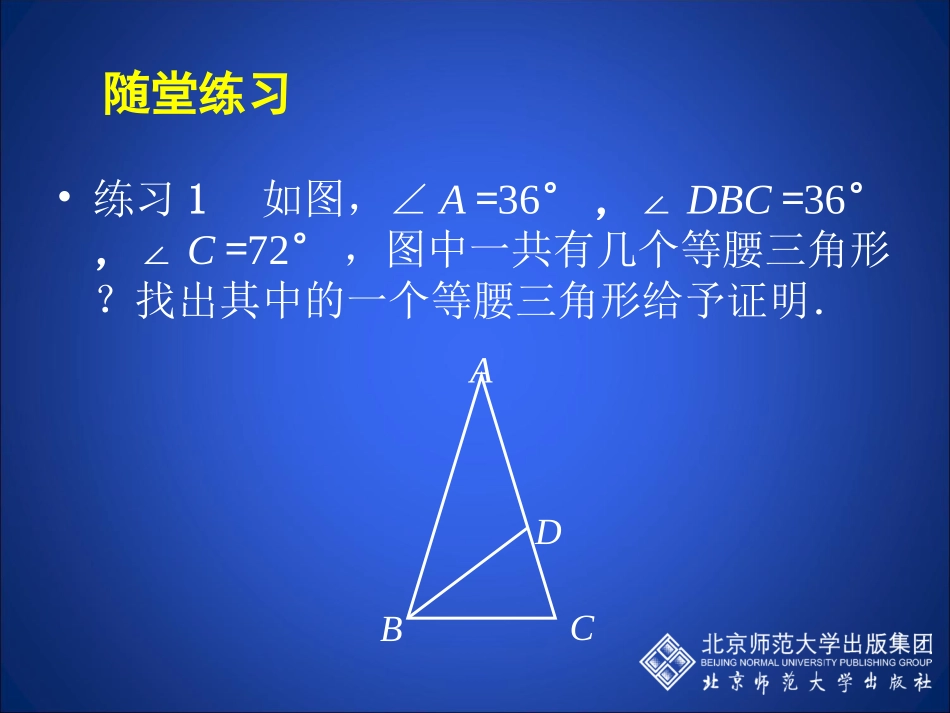
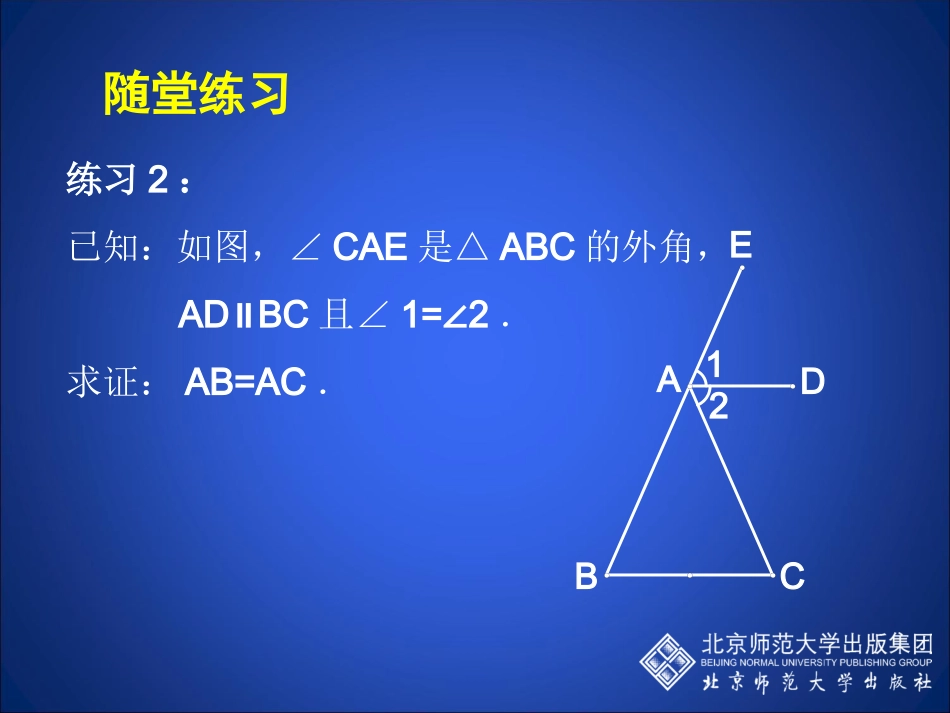
•练习1如图,∠A=36°,∠DBC=36°,∠C=72°,图中一共有几个等腰三角形?找出其中的一个等腰三角形给予证明.ABCD随堂练习练习2:已知:如图,∠CAE是△ABC的外角,ADBC∥且∠1=2∠.求证:AB=AC.随堂练习21BACED•3、如图,∆ABC中,BC=BA,∠A=600,BD是AC边的中线,延长BC到E,使CE=CD,求证:DE=DBEDCAB若DB是AC边上的高,上述结论还成立吗?•4、如图,∆ABC中,∠ABC、∠ACB的平分线交于点O,过点O作DE//BC,分别交AB、AC于点D、E,求证:C∆ADE=AB+ACOEDCBA想一想求证:在一个三角形中,如果两个角不相等,那么这两个角所对的边也不相等.我们来看小明同学的想法:如图,在△ABC中,已知∠B≠C.∠假设AB=AC“”,那么根据等边对等角定理可得∠C=B∠,但已知条件是∠B≠C∠.“∠C=B”∠“与已知条件∠B≠C”∠相矛盾,因此AB≠AC你能理解他的推理过程吗?CBA再例如,我们要证明△ABC中不可能有两个直角,也可以采用这位同学的证法.假设有两个角是直角,不妨设∠A=90°,∠B=90°,可得∠A+B=180°∠,但△ABC中∠A+B+C=180°∠∠“∠A+B=180°”∠“与∠A+B+C=180°”∠∠相矛盾,因此△ABC中不可能有两个直角.上面的证法有什么共同的特点呢?在上面的证法中,都是先假设命题的结论不成立,然后由此推导出了与已知或公理或已证明过的定理相矛盾,从而证明命题的结论一定成立.我们把它叫做反证法.例1.证明:如果a1,a2,a3,a4,a5都是正数,且a1+a2+a3+a4+a5=1,那么,这五个数中至少有一个大于或等于1/5.用反证法来证:证明:假设这五个数全部小于1/5,那么这五个数的和a1+a2+a3+a4+a5就小于1.这与已知这五个数的和a1+a2+a3+a4+a5=1相矛盾.因此假设不成立,原命题成立,即这五个数中至少有下个大于或等于1/5.隋堂练习111.用反证法证明:一个三角形中不能有两个角是钝角已知:△ABC.求证:∠A、∠B、∠C中不能有两个角是钝角.在△ABC中,AB≠AC,求证:∠B≠∠CABC证明:假设,则()这与矛盾.假设不成立.∴.∠B=∠CAB=AC等角对等边已知AB≠AC∠B≠∠C2感受反证法:3求证:两条直线相交只有一个交点。已知:如图两条相交直线a、b。求证:a与b只有一个交点。abA●A,●求证:在一个三角形中,至少有一个内角小于或等于60°。已知:△ABC求证:△ABC中至少有一个内角小于或等于60°451、试说出下列命题的反面:(1)a是实数。(2)a大于2。(3)a小于2。(4)至少有2个(5)最多有一个(6)两条直线平行2、用反证法证明“若a2≠b2,则a≠b”的第一步是。3、用反证法证明“如果一个三角形没有两个相等的角,那么这个三角形不是等腰三角形”的第一步a不是实数a小于或等于2a大于或等于2没有两个一个也没有两直线相交假设a=b假设这个三角形是等腰三角形