南京市高三数学二轮专题复习讲义立体几何 人教版VIP免费

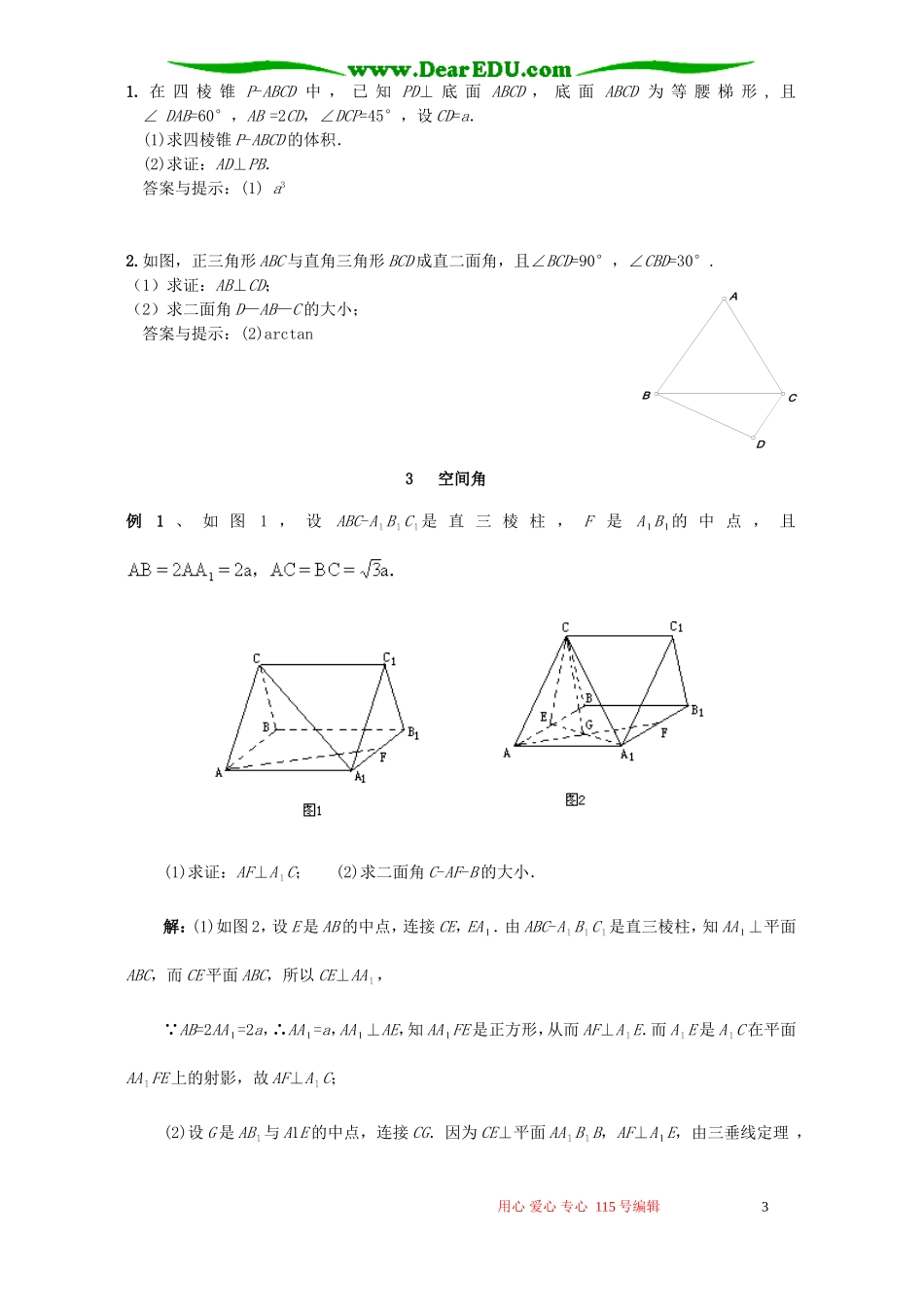
南京市高三数学二轮专题复习讲义立体几何1平行关系例题讲解：例1：已知四面体ABCD中，M、N分别是△ABC和△ACD的重心，求证：(1)MN∥平面ABD；(2)BD∥平面CMN。答案与提示：连CM、CN分别交AB、AD于E、F，连EF，易证MN∥EF∥BD例2.已知边长为10的等边三角形ABC的顶点A在平面α内，顶点B、C在平面α的上方，BD为AC边上的中线，B、C到平面α的距离BB1=2，CC1=4．(1)求证：BB1∥平面ACC1(2)求证：BD⊥平面ACC1(3)求四棱锥A-BCC1B1的体积答案与提示：（3）30例3.已知PA⊥平面ABCD，四边形ABCD是矩形，M、N分别是AB、PC的中点.(1)求证：MN∥平面PAD；(2)求证：MN⊥CD；(3)若平面PCD与平面ABCD所成二面角为θ，问能否确定θ的值，使得MN是异面直线AB与PC的公垂线.答案与提示：（3）45°备用题如图,在三棱锥P-ABC中，PA⊥面ABC，△ABC为正三角形，D、E分别为BC、AC的中点，设AB=2PA=2，(1)如何在BC上找一点F，使AD∥平面PEF？说明理由；(2)对于(1)中的点F，求二面角P-EF-A的大小；答案与提示：（1）F为CD中点（2）arctan2作业在正四棱柱ABCD-A1B1C1D1中，AA1=AB，点E、M分别为A1B、C1C的中点，过A1，B，M三点的平面交C1D1于点N。(1)求证：EM∥平面ABCD；用心爱心专心115号编辑1DCBMANP(2)求二面角B-A1N-B1的正切值。答案与提示：（2）arctan2垂直关系例题讲解：例1：如图,在三棱锥P-ABC中，AB=BC=CA，PA⊥底面ABC，D为AB的中点．(1)求证：CD⊥PB；(2)设二面角A-PB-C的平面角为α，且tanα=，若底面边长为1，求三棱锥P-ABC的体积．答案与提示：（2）例2：已知ABCD—A1B1C1D1是棱长为a的正方体，E、F分别是棱AA1和CC1的中点，G是A1C1的中点．(1)求证平面BFD1E⊥平面BGD1；(2)求点G到平面BFD1E的距离；(3)求四棱锥A1-BFD1E的体积．答案与提示：（2）a(3)a3例3：四边形ABCD中．AD∥BC，AD=AB，∠BCD=45°，∠BAD=90°，将△ABD沿对角线BD折起，记折起点A的位置为P，且使平面PBD⊥平面BCD．(1)求证：CD⊥平面PBD；(2)求证：平面PBC⊥平面PDC；(3)求二面角P—BC—D的大小．答案与提示：(2)先证PB⊥面PCD(3)arctan备用题在三棱锥S-ABC中，已知SA=4，AB=AC，BC=3,∠SAB=∠SAC=45°,SA与底面ABC所的角为30°.(1)求证：SA⊥BC；(2)求二面角S—BC—A的大小；(3)求三棱锥S—ABC的体积．答案与提示：(2)arctan(3)9作业用心爱心专心115号编辑2BAPDCSCCBAA1.在四棱锥P-ABCD中，已知PD⊥底面ABCD，底面ABCD为等腰梯形,且∠DAB=60°，AB=2CD，∠DCP=45°，设CD=a．(1)求四棱锥P-ABCD的体积．(2)求证：AD⊥PB．答案与提示：(1)a32.如图，正三角形ABC与直角三角形BCD成直二面角，且∠BCD=90°，∠CBD=30°.（1）求证：AB⊥CD；（2）求二面角D—AB—C的大小；答案与提示：(2)arctan3空间角例1、如图1，设ABC-ABC是直三棱柱，F是AB的中点，且(1)求证：AF⊥AC；(2)求二面角C-AF-B的大小．解：(1)如图2，设E是AB的中点，连接CE，EA．由ABC-ABC是直三棱柱，知AA⊥平面ABC，而CE平面ABC，所以CE⊥AA， AB=2AA=2a，∴AA=a，AA⊥AE，知AAFE是正方形，从而AF⊥AE．而AE是AC在平面AAFE上的射影，故AF⊥AC；(2)设G是AB与A1E的中点，连接CG．因为CE⊥平面AABB，AF⊥AE，由三垂线定理，用心爱心专心115号编辑3ABCDCG⊥AF，所以∠CGE就是二面角C-AF-B的平面角． AAFE是正方形，AA=a，∴，∴，∴tan∠CGE=，∠CGE＝，从而二面角C-AF-B的大小为。例2、一条长为2的线段夹在互相垂直的两个平面、之间，AB与成45o角，与成角，过A、B两点分别作两平面交线的垂线AC、BD，求平面ABD与平面ABC所成的二面角的大小．以CD为轴，将平以AB为轴，将平面BCD旋转至与面ABD旋转至与平面ACD共面平面ABC共面图1图2图3解法１、过D点作DE⊥AB于E，过E作EF⊥AB交BC于F(图1)，连结DF，则∠DEF即为二面角D－AB－C的平面角．为计算△DEF各边的长，我们不妨画出两个有关的移出图．在图2中，可计算得DE＝1，EF＝，BF＝＝．在移出图3中， cosB＝＝,在△BDF中，由余弦定理：DF2＝BD2＋BF2－2BD﹒BF﹒cosB＝()2＋()2－2﹒﹒＝．（注：其实，由于AB⊥DE，AB⊥EF，∴AB⊥平面DEF，∴AB⊥DF．又 AC⊥平面，∴AC⊥DF．∴DF⊥平面ABC，∴DF⊥BC，即DF...