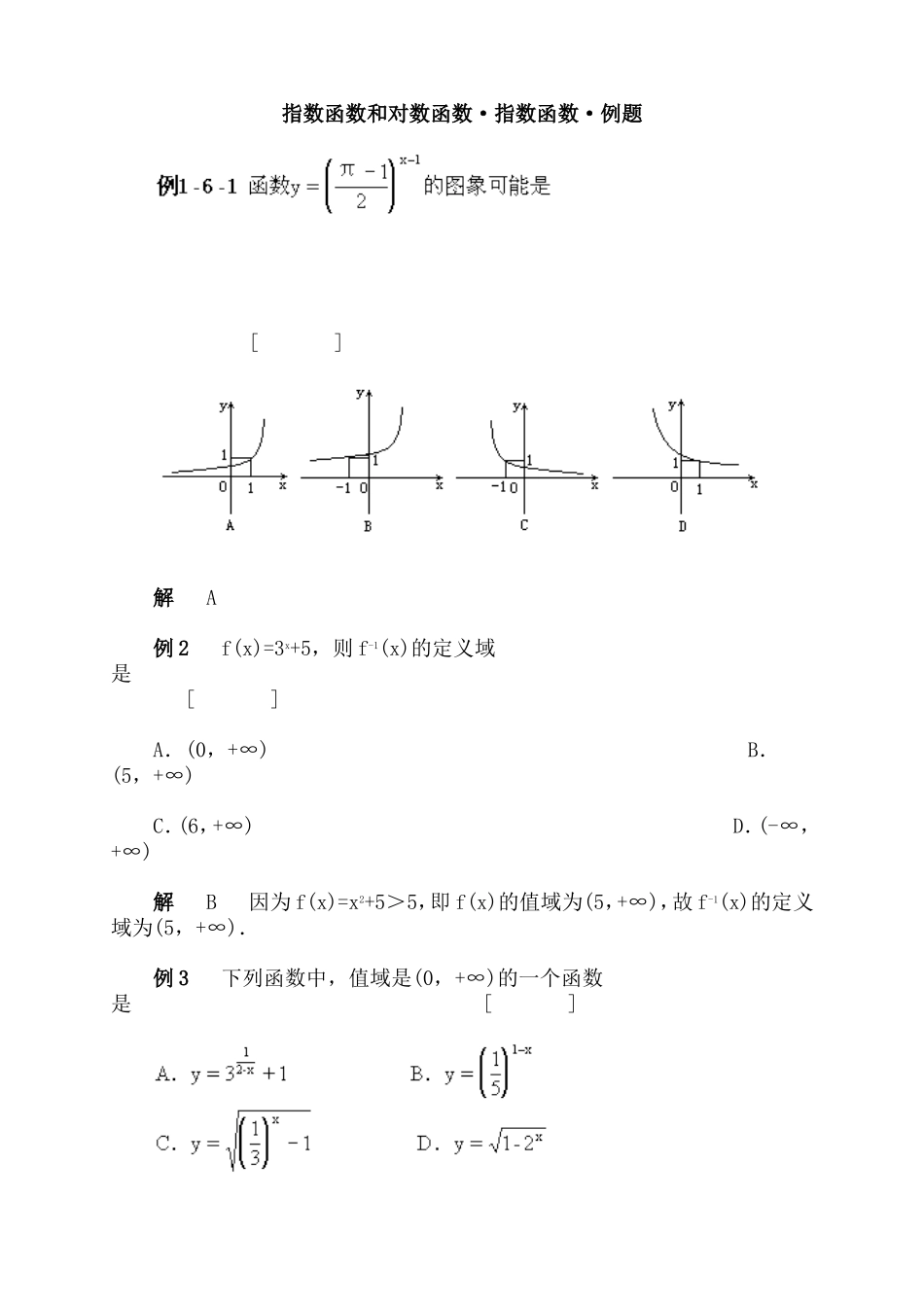
指数函数和对数函数·指数函数·例题[]解A例2f(x)=3x+5,则f-1(x)的定义域是[]A.(0,+∞)B.(5,+∞)C.(6,+∞)D.(-∞,+∞)解B因为f(x)=x2+5>5,即f(x)的值域为(5,+∞),故f-1(x)的定义域为(5,+∞).例3下列函数中,值域是(0,+∞)的一个函数是[]解B例4函数y=(a2-1)x在(-∞,+∞)上是减函数,则a的取值范围是[]例5已知a>b,ab≠0.审查下列不等式.其中恒成立的有[]A.1个B.2个C.3个D.4个解C解(0,1)例7使函数yx2-x-12递减的x的取值范围是______.例8根据不等式确定正数a的取值范围:(1)a-0.3<a0.2,则a∈______;(2)a7.5<a3.9,a∈______;解(1)(1,+∞)(2)(0,1)(3)(0,1)(1)指出函数的奇偶数,并予以证明;(2)求证:对任何x(x∈R且x≠0),都有f(x)>0.所以f(x)是偶函数.(2)当x>0时,2x>1,所以f(x)>0.当x<0时,由f(x)为偶函数,有f(x)=f(-x)>0.所以对一切x∈R,x≠0,恒有f(x)>0.注利用函数的奇偶性常可使解法简化.如本例(2),当x<0时,证明f(x)>0较繁.若注意到f(x)为偶函数,则只须证明,当x>0时f(x)>0,而这是显然的.(1)判断函数f(x)的奇偶性;(2)证明f(x)是区间(-∞,+∞)上的增函数;(3)求函数的值域.解(1)f(x)的定义域为R.又所以f(x)为奇函数.在R上为增函数.[]A.a<b<cB.a<c<bC.b<c<aD.c<b<a解C[]例14对数式loga(x+1),logax2,loga(-x),loga(1-|x|)中的x的[]例15如果f(lgx)=x,则f(3)的值等于[]A.log3B.log310C.l03D.310解C令lgx=3,则x=103.例16若log2x=log3y=log5z>0,则[]解B令log2x=log3y=log5z=k,有x=2k,y=3k,z=5k.于是例17已知ab=M(a>0,b>0,M≠1)且logMb=x,则logMa的值为[]解A因为ab=M,所以logMab=logMM=1,即logMa+logMb=1.但logMb=x,所以logMa=1-x.例18计算:(1)25log53=______例20设M={0,1},N={11-a,log10a,2a,a},是否存在事实上,若lga=1,则a=10.此时11-a=1,从而11-a=lga=1,此与集合元素互异性矛盾.若2a=1,则a=0.此时lga无意义.1,则a=10,从而lga=1,与集合元素互异性矛盾.例22化简:例23设a,b同号,且a2-2ab-9b2=0,求lg(a2+ab-6b2)-lg(a2+4ab+15b2)的值.[]解A[]A.RB.(-∞,-3]C.[8,+∞)D.[3,+∞)解B例26若f(x)=loga|x+1|在(-1,0)内f(x)>0,则f(x)[]A.在(-∞,0)内单调递增B.在(-∞,0)内单调递减C.在(-∞,-1)内单调递减D.在(-∞,-1)内单调递增解D依题设,f(x)的图象关于直线x=-1对称,且0<a<1.画出图象(略)即知D正确.例27已知函数f(x)是奇函数,且当x>0时,f(x)=x2+lg(x+1),那么当x<0时,f(x)的解析式是[]A.-x2-lg(1-x)B.x2+lg(1-x)C.x2-lg(1-x)D.-x2+lg(1-x)解A设x<0,则-x>0,所以f(-x)=(-x)2+lg(-x+1)=x2+lg(1-x)=-f(x)f(x)=-x2-lg(1-x)例28函数y=5x+1的反函数是[]A.y=log5(x+1)B.y=logx5+1C.y=log5(x-1)D.y=log(x-1)5解C解(1)奇函数.∴f(x)为奇函数(2)3.373因为ψ(x)=x2+f(x),又由(1)知,f(x)为奇函数,所以f(-2)=-f(2).所以ψ(-2)=(-2)2+f(-2)=2×22-(22+f(2))=8-ψ(2)=8-4.627=3.373例31若1<x<2,则(log2x)2,log2x2,log2(log2x)的大小关系是______log2(log2x)<(log2x)2<log2x2(1)判断f(x)的奇偶性;(2)已知f(x)存在反函数f-1(x),若f-1(x)<0,求x的取值范围.另一方面,有所以f(x)是奇函数.故当a>1时,x<0;当0<a<1时,x>0.例33已知常数a,b满足a>1>b>0,若f(x)=lg(ax-bx),(1)求y=f(x)的定义域;(2)证明y=f(x)在其定义域内是增函数;(3)若f(x)恰在(1,+∞)上恒取正值,且f(2)=lg2,求a,b的值.(2)任取x1,x2∈(0,+∞),且x1<x2.因为a>1,所以g1(x)=ax是增函数,所以ax1-ax2<0.故f(x)=lg(ax-bx)在(0,+∞)内是增函数.(3)因为f(x)在(1,+∞)内为增函数,所以对于x∈(1,+∞)内每一个x值都有f(x)>f(1).要使f(x)恰在(1,+∞)上恒取正值,即f(x)>0只须f(1)=0.于是f(1)=lg(a-b)=0,得a-b=1.又f(2)=lg2,所以lg(a2-b2)=lg2,所以a2-b2=2,即(a+b)(a-b)=2.而a-b=1,所以a+b=2.例34设0<x<1,a>0且a≠1,试比较|loga(1-x)|与|loga(1+x)|的大小.解作差比较.因为0<x<1,所以0<1-x<1,1<1+x<2...