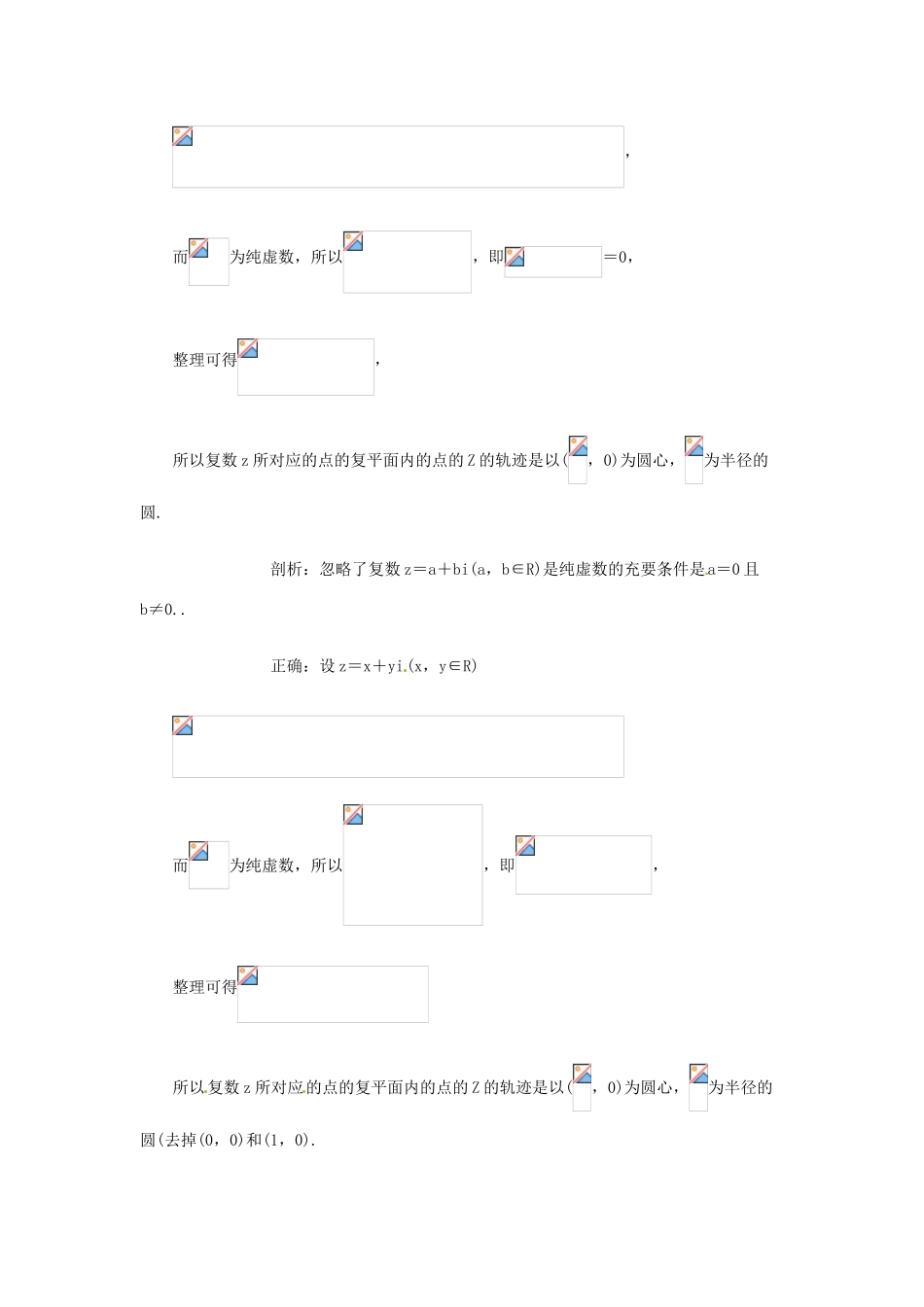
复数加、减法的几何意义易错点主标题:复数加、减法的几何意义易错点副标题:从考点分析复数加、减法的几何意义在高考中的易错点,为学生备考提供简洁有效的备考策略。关键词:复数加、减法,几何意义,易错点难度:3重要程度:4内容:一、向量减法的几何意义记错而致错【例1】已知向量对应的复数为3-2i,向量对应的复数为-4-i,则对应的复数为().A.-1-iB.7-iC.-7+iD.1+i错解:B.剖析:向量,代入对应的复数相减可得出(-4-i)-(3-2i)=-7+i,注意向量的减法的几何意义是指向被减的向量.正解:选C.二、忽略了复数的几何意义而致错【例2】若为纯虚数,则复数z所对应的复平面内的点的Z的轨迹是什么?.错解:设z=x+yi(x,y∈R),,而为纯虚数,所以,即=0,整理可得,所以复数z所对应的点的复平面内的点的Z的轨迹是以(,0)为圆心,为半径的圆.剖析:忽略了复数z=a+bi(a,b∈R)是纯虚数的充要条件是a=0且b≠0..正确:设z=x+yi(x,y∈R)而为纯虚数,所以,即,整理可得所以复数z所对应的点的复平面内的点的Z的轨迹是以(,0)为圆心,为半径的圆(去掉(0,0)和(1,0).三、复数的“模”与“绝对值”混淆而致错【例3】满足不等式的复数z在复平面内对应的点Z的轨迹.错解:原不等式,∵,∴<2,∴-2<z-2<2,即0<z<4.剖析:这种解法的错误在于未注意到“复数集中。任意两个不全为实数的复数不能比较大小”,错误的原因是把实数中绝对值的性质|x|<a-a<x<a(a>0)”生搬硬套到复数模中来.正解:原不等式,∵,∴<2且z≠1,复数z在复平面内对应的点Z的轨迹为以点(2,0)为圆心,2为半径的圆内部,且去除点(1,0).