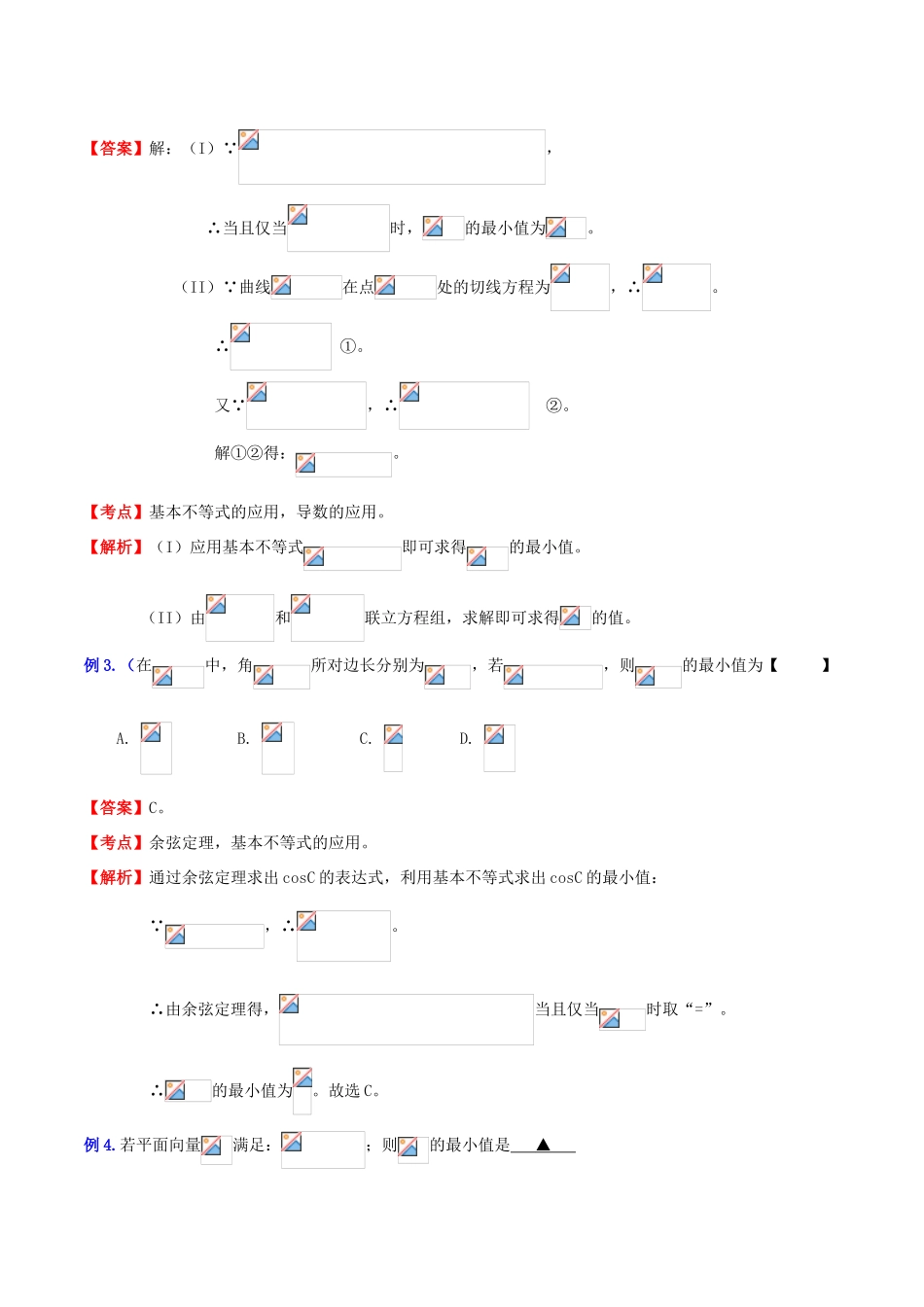
二、应用不等式(含基本不等式)求最值:典型例题:例1.)设(I)求在上的最小值;(II)设曲线在点的切线方程为;求的值。【答案】解:(I)设,则。∴。①当时,。∴在上是增函数。∴当时,的最小值为。②当时,∴当且仅当时,的最小值为。(II)∵,∴。由题意得:,即,解得。【考点】复合函数的应用,导数的应用,函数的增减性,基本不等式的应用。【解析】(I)根据导数的的性质分和求解。(II)根据切线的几何意义列方程组求解。例2.设定义在(0,+)上的函数(Ⅰ)求的最小值;(II)若曲线在点处的切线方程为,求的值。【答案】解:(I)∵,∴当且仅当时,的最小值为。(II)∵曲线在点处的切线方程为,∴。∴①。又∵,∴②。解①②得:。【考点】基本不等式的应用,导数的应用。【解析】(I)应用基本不等式即可求得的最小值。(II)由和联立方程组,求解即可求得的值。例3.(在中,角所对边长分别为,若,则的最小值为【】A.B.C.D.【答案】C。【考点】余弦定理,基本不等式的应用。【解析】通过余弦定理求出cosC的表达式,利用基本不等式求出cosC的最小值:∵,∴。∴由余弦定理得,当且仅当时取“=”。∴的最小值为。故选C。例4.若平面向量满足:;则的最小值是▲来【答案】。【考点】平面向量,基本不等式的应用。【解析】∵,∴。又∵,∴。∴。∴的最小值是。例5.设,,若直线与圆相切,则的取值范围是【】(A)(B)(C)(D)【答案】D。【考点】直线与圆的位置关系,点到直线的距离公式,重要不等式,一元二次不等式的解法【分析】∵直线与圆相切,∴圆心到直线的距离为,∴。又∵,∴,即。∴。设,则,解得。故选D。例6.()已知两条直线:和:,与函数的图像从左至右相交于点A,B,与函数的图像从左至右相交于C,D.记线段AC和BD在X轴上的投影长度分别为,,当m变化时,的最小值为【】A.B.C.D.【答案】B。【考点】数形结合,函数的图象,基本不等式的应用。【解析】如图,在同一坐标系中作出,,图像,由,得,由,得。根据题意得。∵,∴。故选B。