高考数学 命题角度2.1 利用正弦定理和余弦定理解三角形大题狂练 理-人教版高三全册数学试题VIP免费

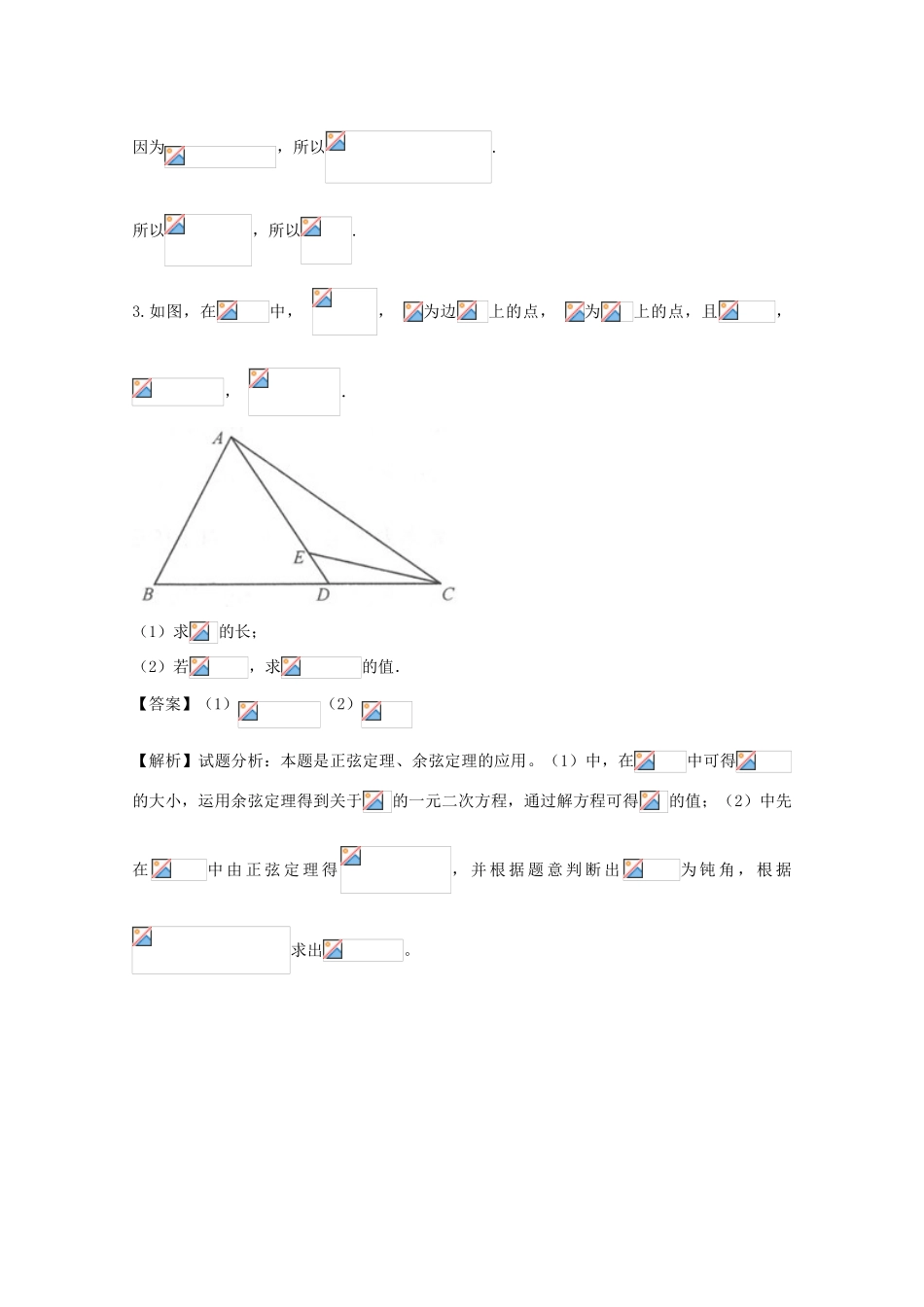
命题角度2.1：利用正弦定理和余弦定理解三角形1.如图中，已知点在边上，且，，，．（1）求的长；（2）求．【答案】（1）；（2）．试题解析：（1）因为，所以，所以．在中，由余弦定理可知，即，解之得或，由于，所以．（2）在中，由正弦定理可知，，又由可知，所以因为，即考点：1．诱导公式；2．正弦定理与余弦定理．2.在，，（1）若，求的长（2）若点在边上，，，为垂足，，求角的值.【答案】（1）；（2）.（2）因为，所以.在中，由正弦定理可得：，因为，所以.所以，所以.3.如图，在中，，为边上的点，为上的点，且，，．（1）求的长；（2）若，求的值．【答案】（1）（2）【解析】试题分析：本题是正弦定理、余弦定理的应用。（1）中，在中可得的大小，运用余弦定理得到关于的一元二次方程，通过解方程可得的值；（2）中先在中由正弦定理得，并根据题意判断出为钝角，根据求出。（2）在中，由正弦定理得，即所以，所以．因为点在边上，所以，而，所以只能为钝角，所以，所以．4.的内角的对边分别为，且．（1）证明：成等比数列；（2）若角的平分线交于点，且，求．【答案】（1）见解析；（2）.【解析】试题分析：（1）利用两角和的余弦函数公式化简已知等式可得sinAsinC=sin2B，由正弦定理可得：b2=ac，即可得证．（2）由已知可得：AD+CD=6，由三角形面积公式可得AD=2CD，从而可求AD=4，CD=2，由（1）可得：b2=36，利用角平分线的性质可得AB=2BC，即c=2a，从而可求a，c的值，进而利用余弦定理可求cosA，即可由余弦定理求得BD的值．试题解析：.解法一:（1）因为，所以，化简可得，由正弦定理得，，故成等比数列.【注】利用角平分线定理得到同样得分，在中由余弦定理可得，，在中由余弦定理可得，，即，求得.解法二：（1）同解法一.（2）同解法一，.在中由余弦定理可得，，在中由余弦定理可得，，即，求得.解法三：（1）同解法一.（2）同解法二，.在中由余弦定理可得，，由于，从而可得，在中由余弦定理可得，，求得，在中由正弦定理可得，，即.【注】若求得的值后，在中应用正弦定理求得的，请类比得分.解法四：（1）同解法一.（2）同解法一，.在中由余弦定理得，，在中由余弦定理得，，因为，所以有，故，整理得，，即.5.在中，角的对边分别为，且.（1）求的值；（2）若成等差数列，且公差大于0，求的值.【答案】（1）；（2）.【解析】试题分析：本题主要考查解三角形中的正弦定理与数列的综合问题、利用正弦定理求三角函数值、等差数列的性质、三角函数值问题等基础知识，同时考查运算转化能力和计算能力.第一问，根据正弦定理将边转换成角，即可得到；第二问，利用等差中项的概念得，再利用正弦定理将边转换成角，得到，设，两式联立，利用平方关系和两角和的余弦公式，得到，再利用内角和与诱导公式，将转化成，解方程求出的值，即的值.试题解析：（Ⅰ）由，根据正弦定理得，所以．4分（Ⅱ）由已知和正弦定理以及（Ⅰ）得．①设，②①2＋②2，得．③7分又，，所以，，故．10分代入③式得．因此．考点：1.正弦定理；2.等差中项；3.两角和的余弦公式；4.诱导公式.6.在中，角所对的边分别为，且，．（Ⅰ）若，求角的正弦值及的面积；（Ⅱ）若在线段上，且，，求的长．【答案】（I），面积为；（II）.【解析】试题分析：(1)首先利用正弦定理求得，然后求得，结合面积公式可得的面积为.(2)利用题意设出边长，结合余弦定理列出方程，最后利用勾股定理可得的长为.（Ⅱ）设，则，，又，，在中，由余弦定理得，即，解得，则，所以，在直角中，．7.如图，在平面四边形中，已知，，，在边上取点，使得，连接，若，.（1）求的值；（2）求的长.【答案】（1）（2）【解析】试题分析：（1）在中，直接由正弦定理求出；（2）在中，，，可求出，在中，直接由余弦定理可求得.试题解析：（1）在中，据正弦定理，有. ，，，∴.（2）由平面几何知识，可知，在中， ，，∴.∴.在中，据余弦定理，有∴点睛：此题考查了正弦定理、余弦定理的应用，利用正弦、余弦定理可以很好得解决了三角形的边角关系，熟练掌握定理是解本题的关键．在中，涉及三边三角，知三（除已知三角外）求三，可解出三角形，...