高考数学必胜秘诀（04）三角函数 VIP免费

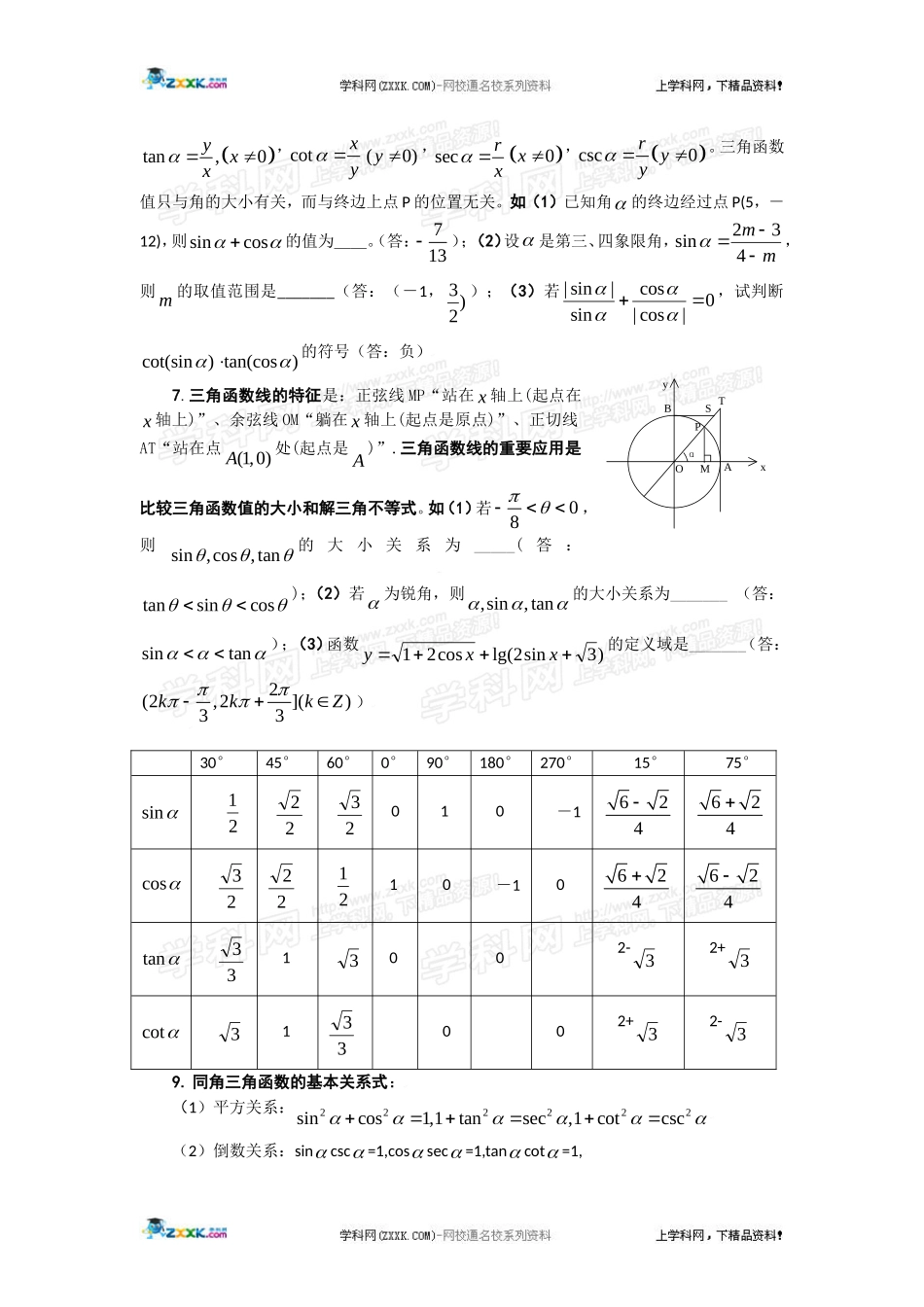
高考数学必胜秘诀（4）三角函数1、角的概念的推广：平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角，按顺时针方向旋转所形成的角叫负角，一条射线没有作任何旋转时，称它形成一个零角。射线的起始位置称为始边，终止位置称为终边。2、象限角的概念：在直角坐标系中，使角的顶点与原点重合，角的始边与x轴的非负半轴重合，角的终边在第几象限，就说这个角是第几象限的角。如果角的终边在坐标轴上，就认为这个角不属于任何象限。3.终边相同的角的表示：（1）终边与终边相同(的终边在终边所在射线上)2()kkZ，注意：相等的角的终边一定相同，终边相同的角不一定相等.如与角1825的终边相同，且绝对值最小的角的度数是＿＿＿，合＿＿＿弧度。（答：25；536）（2）终边与终边共线(的终边在终边所在直线上)()kkZ.（3）终边与终边关于x轴对称2()kkZ.（4）终边与终边关于y轴对称2()kkZ.（5）终边与终边关于原点对称2()kkZ.（6）终边在x轴上的角可表示为：,kkZ；终边在y轴上的角可表示为：,2kkZ；终边在坐标轴上的角可表示为：,2kkZ.如的终边与6的终边关于直线xy对称，则＝____________。（答：Zkk,32）4、与2的终边关系：由“两等分各象限、一二三四”确定.如若是第二象限角，则2是第_____象限角（答：一、三）5.弧长公式：||lR，扇形面积公式：211||22SlRR，1弧度(1rad)57.3.如已知扇形AOB的周长是6cm，该扇形的中心角是1弧度，求该扇形的面积。（答：22cm）6、任意角的三角函数的定义：设是任意一个角，P(,)xy是的终边上的任意一点（异于原点），它与原点的距离是220rxy，那么sin,cosyxrr，tan,0yxx，cotxy(0)y，secrx0x，csc0ryy。三角函数值只与角的大小有关，而与终边上点P的位置无关。如（1）已知角的终边经过点P(5，－12)，则cossin的值为＿＿。（答：713）；（2）设是第三、四象限角，mm432sin，则m的取值范围是_______（答：（－1，)23）；（3）若0|cos|cossin|sin|，试判断)tan(cos)cot(sin的符号（答：负）7.三角函数线的特征是：正弦线MP“站在x轴上(起点在x轴上)”、余弦线OM“躺在x轴上(起点是原点)”、正切线AT“站在点(1,0)A处(起点是A)”.三角函数线的重要应用是比较三角函数值的大小和解三角不等式。如（1）若08，则sin,cos,tan的大小关系为_____(答：tansincos)；（2）若为锐角，则,sin,tan的大小关系为_______（答：sintan）；（3）函数)3sin2lg(cos21xxy的定义域是_______（答：2(2,2]()33kkkZ）8.特殊角的三角函数值：30°45°60°0°90°180°270°15°75°sin212223010－1624624cos23222110－10624624tan3313002-32+3cot3133002+32-39.同角三角函数的基本关系式：（1）平方关系：222222sincos1,1tansec,1cotcsc（2）倒数关系：sincsc=1,cossec=1,tancot=1,yTAxαBSOMP（3）商数关系：sincostan,cotcossin同角三角函数的基本关系式的主要应用是，已知一个角的三角函数值，求此角的其它三角函数值。在运用平方关系解题时，要根据已知角的范围和三角函数的取值，尽可能地压缩角的范围，以便进行定号；在具体求三角函数值时，一般不需用同角三角函数的基本关系式，而是先根据角的范围确定三角函数值的符号，再利用解直角三角形求出此三角函数值的绝对值。如（1）函数sintancoscoty的值的符号为____（答：大于0）；（2）若220x，则使xx2cos2sin12成立的x的取值范围是____（答：[0,]4],43[）；（3）已知53sinmm，)2(524cosmm，则tan＝____（答：125）；（4）已知11tantan，则cossincos3si...