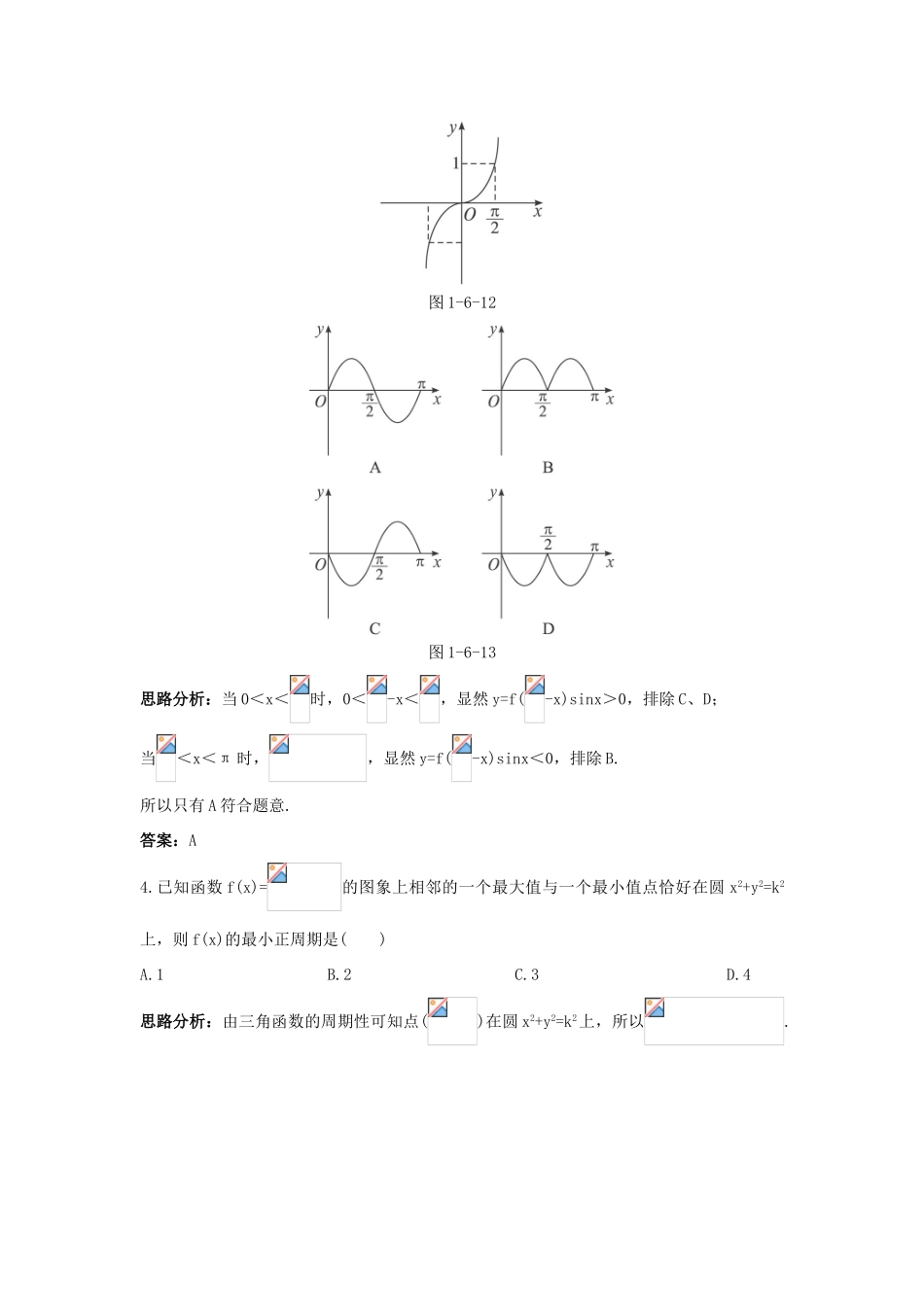
1.6三角函数模型的简单应用更上一层楼基础•巩固1.若函数f(x)=3sin(ωx+φ)对任意实数x,都有f(x+)=f(-x),则f()等于()A.0B.3C.-3D.3或-3思路分析:由f(x+)=f(-x),可知函数f(x)关于直线x=对称,所以f()=±3.答案:D2.设函数y=sin(ωx+φ)+1(ω>0)的一段图象如图1-611所示,则周期T、初相φ的值依次为()A.π,B.2π,C.π,D.2π,图1-6-11思路分析:T=2(-)=π,所以此时y=sin(2x+φ)+1,因为(,0)是使函数f(x)=sin(2x+φ)取最小值的点,所以2x+φ=+2kπ,φ=-2×-+2kπ=+2kπ,k∈Z,可取φ=.答案:C3.已知函数y=f(x)的图象如图1-6-12,则函数y=f(-x)sinx在[0,π]上的大致图象是()图1-6-12图1-6-13思路分析:当0<x<时,0<-x<,显然y=f(-x)sinx>0,排除C、D;当<x<π时,,显然y=f(-x)sinx<0,排除B.所以只有A符合题意.答案:A4.已知函数f(x)=的图象上相邻的一个最大值与一个最小值点恰好在圆x2+y2=k2上,则f(x)的最小正周期是()A.1B.2C.3D.4思路分析:由三角函数的周期性可知点()在圆x2+y2=k2上,所以.解得k=±2.此时,函数的最小正周期是.答案:D5.函数y=sin(2x+)与y轴最近的对称轴方程是K__________.思路分析:函数y=sin(2x+)的对称轴方程是2x+=kπ+,即x=kπ+,k∈Z,显然k=0时,x=,它离y轴最近.答案:x=6.函数y=sin(kx+)的周期为T,且T∈(1,3),则最大正整数k=___________.思路分析:由题意可知1<<3,因为k∈N,所以k=3,4,5,6.此时k=6.答案:6综合•应用7.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<)的图象在y轴上的截距为1,它在y轴右侧的第一个最大值点和最小值点分别为(x0,2)和(x0+3π,-2).(1)求f(x)的解析式;(2)将y=f(x)图象上所有点的横坐标缩短到原来的倍(纵坐标不变),然后再将所得图象向x轴正方向平移个单位,得到函数y=g(x)的图象.写出函数y=g(x)的解析式并用列表作图的方法画y=g(x)在长度为一个周期的闭区间上的图象.解:(1)由题意可知A=2,T=2[(x0+3π)-x0]=6π.又由ω>0,=6π,得ω=,此时f(x)=2sin(x+φ).又因为该函数经过点(0,1),所以2sinφ=1,即sinφ=因为|φ|<,所以φ=.所以f(x)=2sin(x+).(2)由题意知g(x)=2sin(x-),该函数的周期T=2π,我们先画出它在长度为一个周期的闭区间上的简图.列表:xx-0π2π2sin(x-)020-20描点画图:图1-6-148.设函数f(x)=sin(ωx+φ)(),ω>0,给出以下四个论断:①它的图象关于直线x=对称;②它的图象关于点(,0)对称;③它的周期是π;④它在区间[,0]上是增函数.以其中的两个论断作为条件,余下的两个论断作为结论,写出你认为正确的两个命题,并对其中一个命题加以证明.解:由题可知:若①③成立,则②④成立;若②③成立,则①④成立.现在我们以①③为条件求出函数解析式,证明②④成立.因为该函数的周期是π,所以ω==2.又因为该函数关于直线x=对称,所以当x=时,y取最值.由sin(2×+φ)=1或sin(2×+φ)=-1,,得φ=.所以f(x)=sin(2x+).当x=时,因为f()=sin(2×+)=sinπ=0,所以②成立;当x∈[-,0]时,因为(2x+)∈[0,],所以f(x)=sin(2x+)是增函数,即④成立,即若①③成立,则②④成立.回顾•展望9.(2006海南统考)设关于x的方程sin(2x+)=在[0,]内有两个不同根α、β,求α+β的值及k的取值范围.思路分析:可在同一坐标系中画出函数y=sin(2x+)及的图象,借助于图象的直观性求解.解:设C:y=sin(2x+),l:,在同一坐标系中作出它们的图象如下图.由图易见当时,即0≤k<1时,直线l与曲线C有两个交点,且两交点的横坐标为α、β,从图象中还可看出α、β关于x=对称,故α+β=.综上,可知0≤k<1,且α+β=.