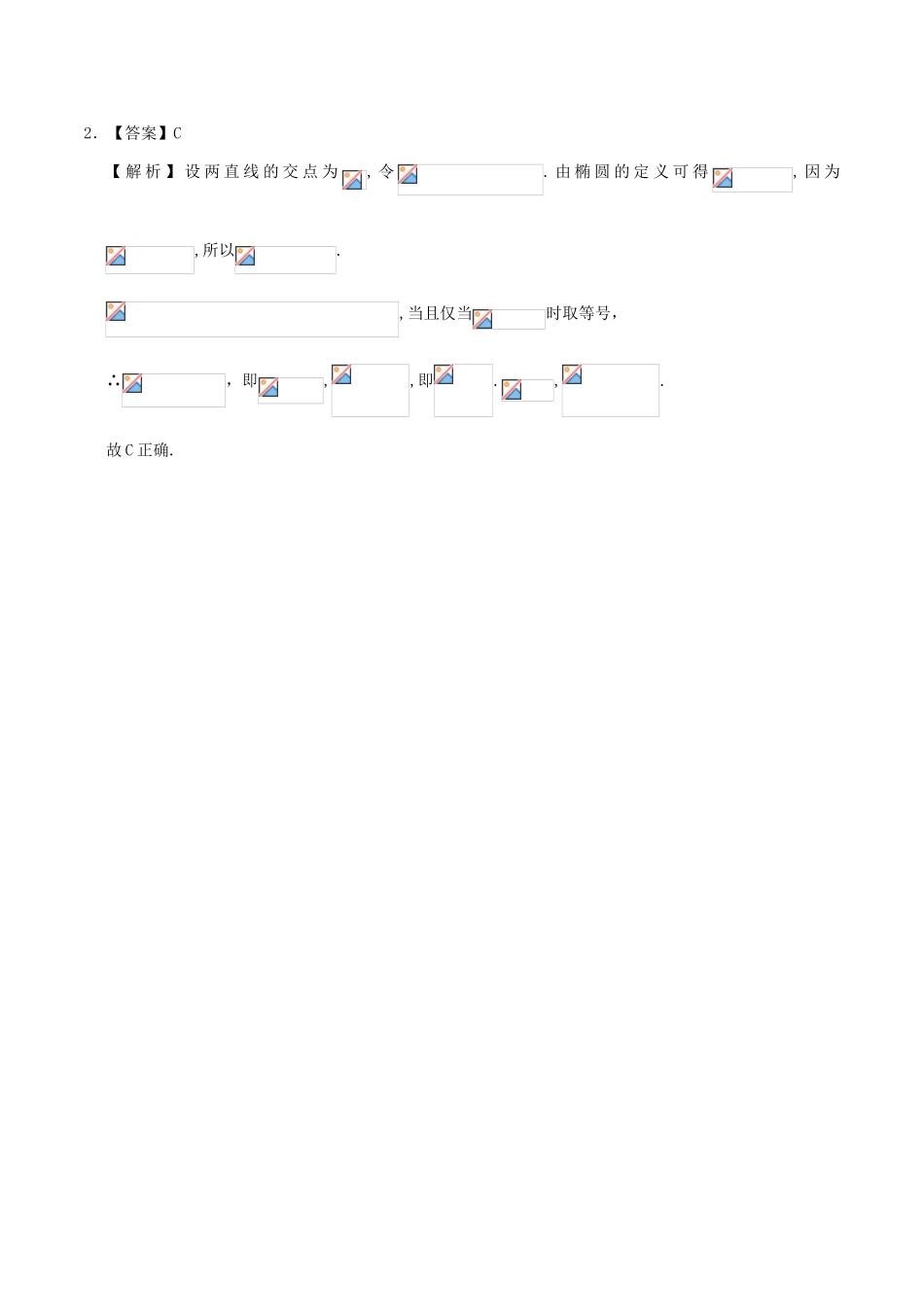
培优练习高考频度:★★★★☆难易程度:★★★☆☆典例在线(2017年高考新课标Ⅲ卷)已知椭圆C:的左、右顶点分别为A1,A2,且以线段A1A2为直径的圆与直线相切,则C的离心率为A.B.C.D.【参考答案】A【解题必备】椭圆的离心率是椭圆最重要的几何性质,求椭圆的离心率(或离心率的取值范围)常见的有两种方法:①求出a,c,代入公式e=;②只需要根据一个条件得到关于a,b,c的齐次式,结合转化为a,c的齐次式,然后等式(不等式)两边分别除以a或a2转化为关于的方程(不等式),解方程(不等式)即可得(的取值范围).学霸推荐1.已知椭圆的左、右焦点分别为,点是椭圆上一点,且,则等于A.B.C.D.2.分别过椭圆的左、右焦点F1、F2所作的两条互相垂直的直线l1、l2的交点在椭圆上,则此椭圆的离心率的取值范围是A.(0,1)B.C.D.【名师点睛】解答本题的关键是搞清楚焦点三角形是直角三角形,求解时充分借助题设条件,先运用勾股定理建立方程,再运用椭圆的定义建立方程,然后再联立这两个方程求得,从而使得问题获解.2.【答案】C【解析】设两直线的交点为,令.由椭圆的定义可得,因为,所以.,当且仅当时取等号,∴,即,,即.,.故C正确.