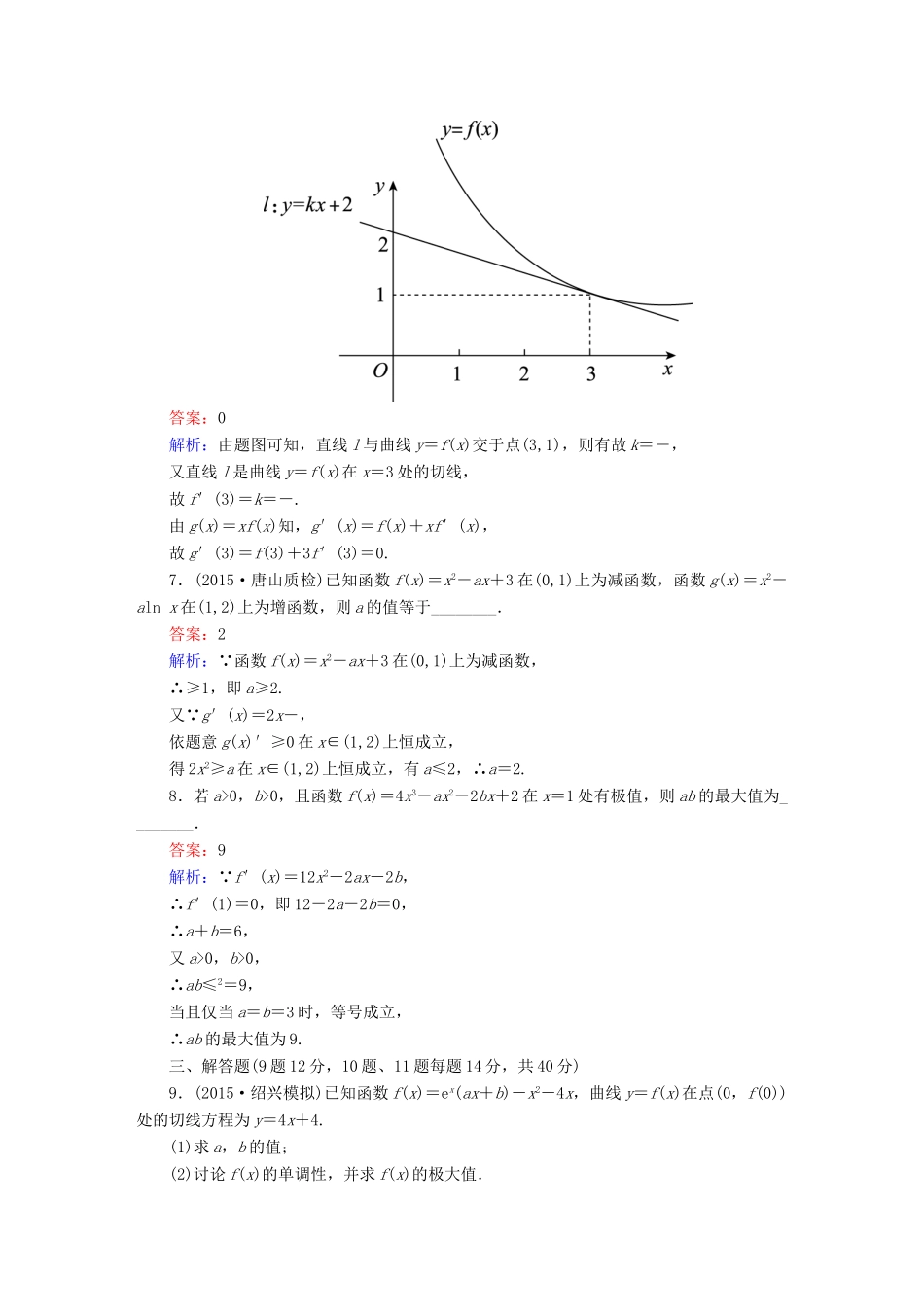
专题限时训练(五)导数的简单应用(时间:45分钟分数:80分)一、选择题(每小题5分,共25分)1.(2015·菏泽模拟)已知函数f(x)=x2-cosx,则f(0.6),f(0),f(-0.5)的大小关系是()A.f(0)0,所以f(x)在(0,1)上是增函数,所以f(0)0,b>0,且函数f(x)=4x3-ax2-2bx+2在x=1处有极值,则ab的最大值为________.答案:9解析: f′(x)=12x2-2ax-2b,∴f′(1)=0,即12-2a-2b=0,∴a+b=6,又a>0,b>0,∴ab≤2=9,当且仅当a=b=3时,等号成立,∴ab的最大值为9.三、解答题(9题12分,10题、11题每题14分,共40分)9.(2015·绍兴模拟)已知函数f(x)=ex(ax+b)-x2-4x,曲线y=f(x)在点(0,f(0))处的切线方程为y=4x+4.(1)求a,b的值;(2)讨论f(x)的单调性,并求f(x)的极大值.解:(1)f′(x)=ex(ax+b)+aex-2x-4=ex(ax+a+b)-2x-4, y=f(x)在(0,f(0))处的切线方程为y=4x+4,∴f′(0)=a+b-4=4,f(0)=b=4,∴a=4,b=4.(2)由(1)知,f′(x)=4ex(x+2)-2(x+2)=2(x+2)(2ex-1),令f′(x)=0,得x=-2或ln,列表:x(-∞,-2)-...