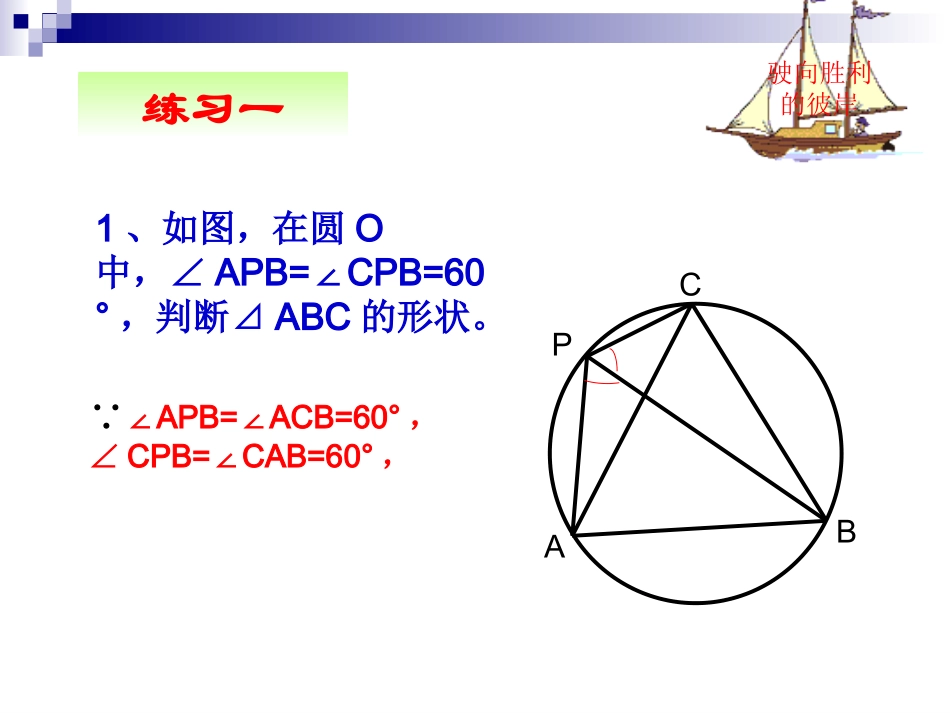
1.1.圆周角定义圆周角定义::顶点在圆上顶点在圆上,,并且并且两边都和圆两边都和圆相交相交的角叫圆周角的角叫圆周角..2.2.一条弧所对的圆周角等于他所对的圆心角的一半。一条弧所对的圆周角等于他所对的圆心角的一半。3.3.同弧或等弧所对的圆周角相等;同弧或等弧所对的圆周角相等;半圆或直径所对的圆周角是半圆或直径所对的圆周角是90°90°;;9090度的圆周角所对的弦是直径。度的圆周角所对的弦是直径。知识回顾知识回顾驶向胜利的彼岸1、如图,在圆O中,∠APB=CPB=60∠°,判断⊿ABC的形状。ACBP∵∠APB=ACB=60°∠,∠CPB=CAB=60°∠,练习一2.AB是⊙O的直径,BD是⊙O的弦,延长BD到点C,使CD=BD,连接AC.判断AB与AC的大小有什么关系?为什么?ABCD练习一∵AB是直径∴∠ADB=90°即ADBC⊥驶向胜利的彼岸练习一●OBAC3、如图,∠AOC=130°,则∠B=()度。如图,⊙O的直径AB为10cm,弦AC为6cm,ACB的平分线交⊙O于点D,求BC,AD,BD的长.例题剖析解:连接OD,AD,BD,ACBDO22ACAB22610∵AB是⊙O的直径,∴ACB=ADB=90°.在Rt△ABC中,BC===8(cm)如图,⊙O的直径AB为10cm,弦AC为6cm,ACB的平分线交⊙O于点D,求BC,AD,BD的长.例题剖析ACBDO∵CD平分ACB,∴ACD=BCD,∴AOD=BOD.∴AD=BD.在Rt△ABD中,AD2+BD2=AB2,∴AD=BD=AB22=(cm).25在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等吗?为什么?在同圆或等圆中,如果两个圆周角相等,它们所对弧一定相等.C·BOAFGE((驶向胜利的彼岸如图,A、B、C、D四点在⊙O上,则把四边形ABCD叫做圆O的内接四边形,把圆O叫做四边形的外接圆。新概念●OCABD问题:在右图中,∠A+C∠等于多少度?∠B+D∠呢?圆内接四边形的性质定理:圆内接四边形的对角互补。驶向胜利的彼岸BAD1.如图:四边形ABCD内接于⊙O,则BODABDCO70练习二驶向胜利的彼岸练习二●OBAC2、如图,∠AOC=130°,则∠B=()度。3、求证:圆内接平行四边形是矩形。ABCD1.如图,你能设法确定一个圆形纸片的圆心吗?你有多少种方法?与同学交流一下.DABCOOO·方法一方法二方法三方法四AB使用帮助练习三、1、在⊙O中,∠CBD=30°,BDC=20°,∠求∠A1、在⊙O中,∠CBD=30°,BDC=20°,∠求∠A2、如图,在⊙O中,AB为直径,CB=CF,弦CGAB⊥,交AB于D,交BF于E求证:BE=EC⌒⌒⌒⌒2、求证:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(提示:作出以这条边为直径的圆.)·ABCO已知:△ABC,CO为AB边上的中线,求证:△ABC为直角三角形.证明:CO=AB,12以AB为直径作⊙O,∵AO=BO,∴AO=BO=CO.∴点C在⊙O上.又∵AB为直径,∴∠ACB=×180°=90°.1212且CO=AB∴△ABC为直角三角形.2121211.1.圆周角定义圆周角定义::顶点在圆上顶点在圆上,,并且并且两边都和圆相交两边都和圆相交的角叫圆周角的角叫圆周角..2.2.圆周角定理圆周角定理在同圆在同圆((或等圆或等圆))中中,,同弧或等弧所对的圆周角相等同弧或等弧所对的圆周角相等,,都等于该弧所都等于该弧所对的圆心角的一半。对的圆心角的一半。3.3.圆周角定理的推论圆周角定理的推论((11)半圆或直径所对的圆周角是)半圆或直径所对的圆周角是90°90°,,9090度的圆周角所对的弦是直径;度的圆周角所对的弦是直径;((22))在同圆在同圆((或等圆或等圆))中中,相等的圆周角所对的弧相等。,相等的圆周角所对的弧相等。小结小结::4、圆内接四边形的概念5、圆内接四边形的性质定理:圆内接四边形的对角互补。6、直角三角形的一种判定方法:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形。7、分类讨论思想和由特殊到一般(转化)思想。