解析几何(4)VIP免费

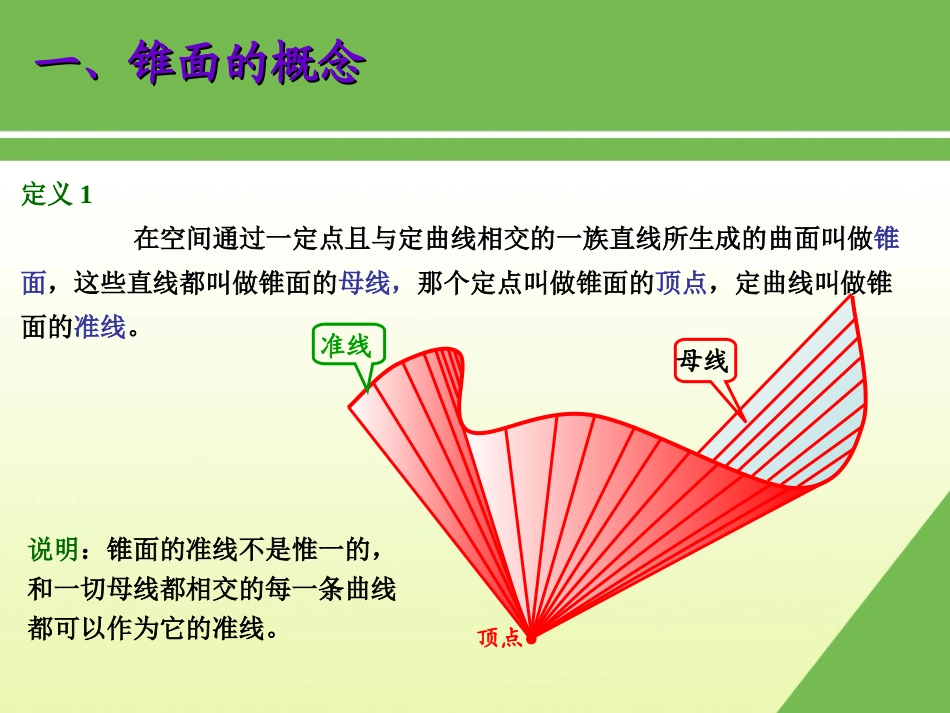
§2§2锥锥面面《《解析几何解析几何》》－－ChapterChapter44ContentsContents一、锥面的概念一、锥面的概念二、锥面的方程二、锥面的方程三、锥面的判定定理三、锥面的判定定理一、锥面的概念一、锥面的概念定义1在空间通过一定点且与定曲线相交的一族直线所生成的曲面叫做锥面，这些直线都叫做锥面的母线，那个定点叫做锥面的顶点，定曲线叫做锥面的准线。顶点准线说明：锥面的准线不是惟一的，和一切母线都相交的每一条曲线都可以作为它的准线。母线二、锥面的方程二、锥面的方程1锥面的一般方程准线，12,,0,,0FxyzFxyz11112111000101010,,0,,0,,0FxyzFxyzFxyzxxyyzzxxyyzz顶点，000,,Axyz取准线上任意一点，1111,,Mxyz2锥面的参数方程已知锥面的准线为，顶点决定的向径为，则锥面的向量式参数方程与坐标式参数方程分别为与，式中为参数,,ruxuyuzu0000,,rxyz�01rvruvr��000111xvxuvxyvyuvyzvzuvz,uvA例1锥面的顶点在原点，且准线为，求锥面的方程22221xyabzc二、锥面的方程二、锥面的方程3.已知圆锥面的轴，顶点，半顶角，求直圆锥面的方程000:xxyyzzLXYZ000,,Axyz02例2已知圆锥面的顶点为，轴垂直于平面，母线与轴成角，试求这圆锥面的方程1,2,3:2210xyz30半顶角lM0Mv0,MMv�或0cos,cosMMv�二、锥面的方程二、锥面的方程定义2’对于正整数，若方程对于任意实数满足，则称方程为次齐次方程.定义2设为实数，对于函数，如果有，（的取值应当使有确定的意义），那么叫做次齐次函数，叫做次齐次方程三、锥面的判定定理三、锥面的判定定理,,0fxyz,,fxyz,,fxyz,,,,ftxtytztfxyztt,,0fxyzntn,,,,nftxtytztfxyz,,0fxyz定理1一个关于的（正数次）齐次方程总表示顶点在坐标原点的锥面。（反之亦然）,,xyz推论关于的（正数次）齐次方程表示顶点在的锥面（反之亦然）000,,xxyyzz000,,xyz例3P1514求以三坐标轴为母线的圆锥面的方程三、锥面的判定定理三、锥面的判定定理