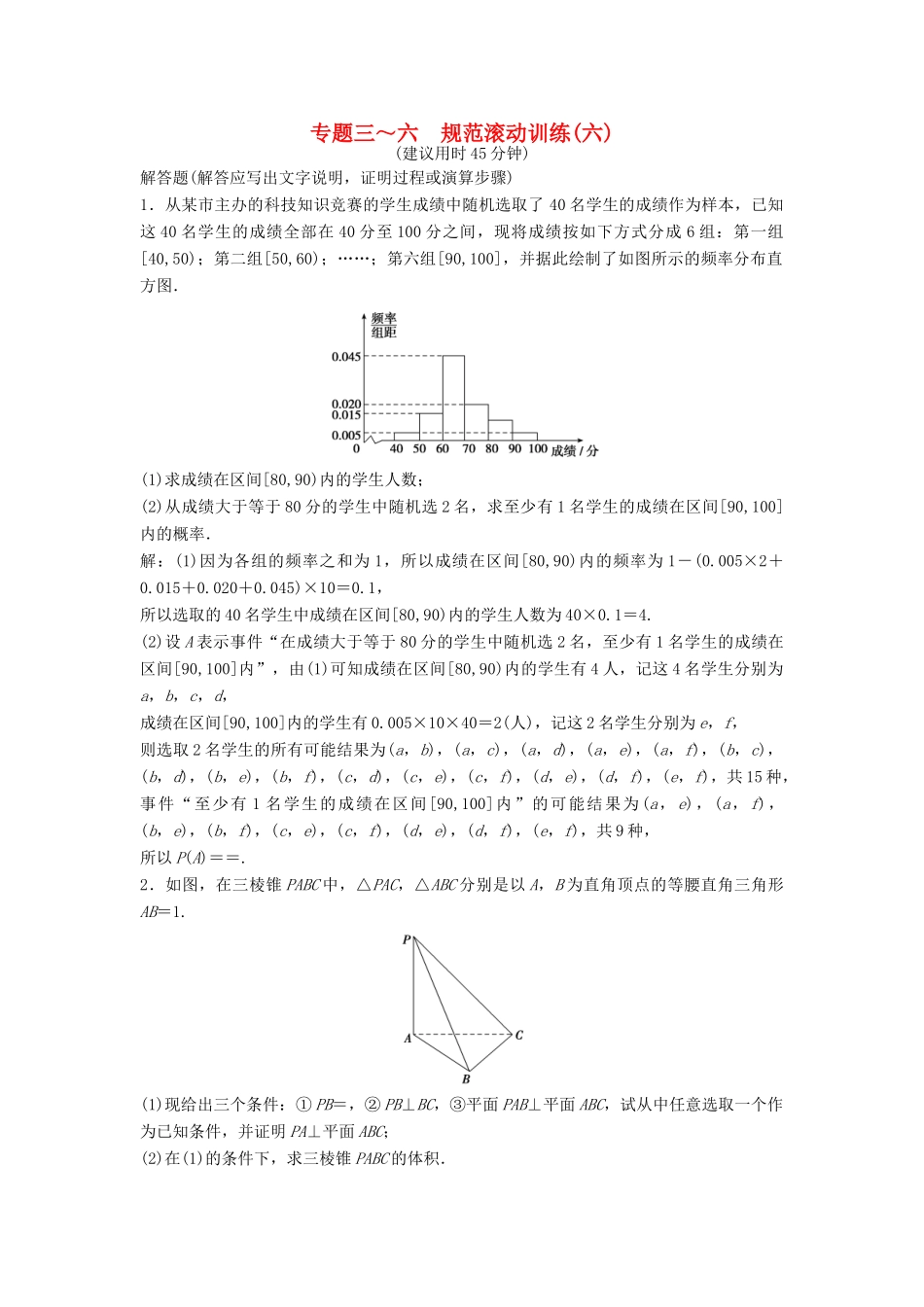
专题三~六规范滚动训练(六)(建议用时45分钟)解答题(解答应写出文字说明,证明过程或演算步骤)1.从某市主办的科技知识竞赛的学生成绩中随机选取了40名学生的成绩作为样本,已知这40名学生的成绩全部在40分至100分之间,现将成绩按如下方式分成6组:第一组[40,50);第二组[50,60);……;第六组[90,100],并据此绘制了如图所示的频率分布直方图.(1)求成绩在区间[80,90)内的学生人数;(2)从成绩大于等于80分的学生中随机选2名,求至少有1名学生的成绩在区间[90,100]内的概率.解:(1)因为各组的频率之和为1,所以成绩在区间[80,90)内的频率为1-(0.005×2+0.015+0.020+0.045)×10=0.1,所以选取的40名学生中成绩在区间[80,90)内的学生人数为40×0.1=4.(2)设A表示事件“在成绩大于等于80分的学生中随机选2名,至少有1名学生的成绩在区间[90,100]内”,由(1)可知成绩在区间[80,90)内的学生有4人,记这4名学生分别为a,b,c,d,成绩在区间[90,100]内的学生有0.005×10×40=2(人),记这2名学生分别为e,f,则选取2名学生的所有可能结果为(a,b),(a,c),(a,d),(a,e),(a,f),(b,c),(b,d),(b,e),(b,f),(c,d),(c,e),(c,f),(d,e),(d,f),(e,f),共15种,事件“至少有1名学生的成绩在区间[90,100]内”的可能结果为(a,e),(a,f),(b,e),(b,f),(c,e),(c,f),(d,e),(d,f),(e,f),共9种,所以P(A)==.2.如图,在三棱锥PABC中,△PAC,△ABC分别是以A,B为直角顶点的等腰直角三角形AB=1.(1)现给出三个条件:①PB=,②PB⊥BC,③平面PAB⊥平面ABC,试从中任意选取一个作为已知条件,并证明PA⊥平面ABC;(2)在(1)的条件下,求三棱锥PABC的体积.解:法一:选取条件①.(1)在等腰直角三角形ABC中,∵AB=1,∴BC=1,AC=.又PA=AC,∴PA=.在△PAB中,AB=1,PA=,PB=,∴AB2+PA2=PB2,∴∠PAB=90°,即PA⊥AB,又PA⊥AC,AB∩AC=A,∴PA⊥平面ABC.(2)由(1)可知PA⊥平面ABC.∴V三棱锥PABC=PA·S△ABC=×××12=.法二:选取条件②.(1)∵PB⊥BC,又AB⊥BC,且PB∩AB=B,∴BC⊥平面PAB.又PA⊂平面PAB,∴BC⊥PA,又PA⊥AC,BC∩AC=C,∴PA⊥平面ABC.(2)由(1)可知PA⊥平面ABC.∵AB=BC=1,AB⊥BC,∴AC=PA=.∴V三棱锥PABC=×AB×BC×PA=××1×1×=.法三:选取条件③.(1)∵平面PAB⊥平面ABC,平面PAB∩平面ABC=AB,BC⊂平面ABC,BC⊥AB,∴BC⊥平面PAB.又PA⊂平面PAB,∴BC⊥PA,又PA⊥AC,BC∩AC=C,∴PA⊥平面ABC.(2)由(1)可知PA⊥平面ABC.∵AB=BC=1,AB⊥BC,∴AC=PA=.∴V三棱锥PABC=×AB×BC×PA=××1×1×=.3.已知圆心为C的圆满足下列条件:圆心C位于y轴的正半轴上,圆C与x轴交于A,B两点,|AB|=4,点B到直线AC的距离为.(1)求圆C的标准方程;(2)若直线y=kx-1(k∈R)与圆C交于M,N两点,OM·ON=-2(O为坐标原点),求k的值.解:(1)设圆C:x2+(y-a)2=r2(a>0,r>0),圆心C(0,a),依题意不妨设A(-2,0),B(2,0),所以直线AC的方程为ax-2y+2a=0,因为点B到直线AC的距离为,所以=,解得a=±1,因为a>0,所以a=1,所以r=|AC|=,所以圆C的标准方程为x2+(y-1)2=5.(2)设M(x1,y1),N(x2,y2),又直线y=kx-1与圆C交于M,N两点,联立,消去y得(1+k2)x2-4kx-1=0.Δ=(-4k)2+4(1+k2)=4(5k2+1)>0恒成立,即直线与圆恒有两个不同的交点.由根与系数的关系知x1+x2=,x1x2=,所以y1y2=(kx1-1)(kx2-1)=k2x1x2-k(x1+x2)+1=-+1=,因为OM·ON=-2,所以x1x2+y1y2=+==-2,解得k=±1.4.已知函数f(x)=(e为自然对数的底数)在x=-1处的切线方程为ex-y+e=0.(1)求实数a,b的值;(2)若存在不相等的实数x1,x2,使得f(x1)=f(x2),求证:x1+x2>0.解:∵f(x)=∴f′(x)=.(1)因为函数f(x)在x=-1处的切线方程为ex-y+e=0,所以,所以,解得(2)由(1)可知,f′(x)=-.当x变化时,f′(x),f(x)的变化情况如下表:x(-∞,0)0(0,+∞)f′(x)+0-f(x)单调递增1单调递减不妨设x1<x2,因为f(x1)=f(x2),所以x1<0<x2,则-x1>0.记g(x)=f(-x)-f(x),即g(x)=(1-x)ex-,所以g′(x)=-ex+(1-x)ex+=-xex+=.当x变化时,g′(x),g(x)的变化情况如下表:x(-∞,0)0(0,+∞)g′(x)-0-g(x)单调递减0单调递减所以g(x1)>g(0)=0,故f(-x1)>f(x1).所以f(-x1)>f(x2).因为f(x)在(0,+∞)上为减函数,所以-x1<x2,故x1+x2>0.