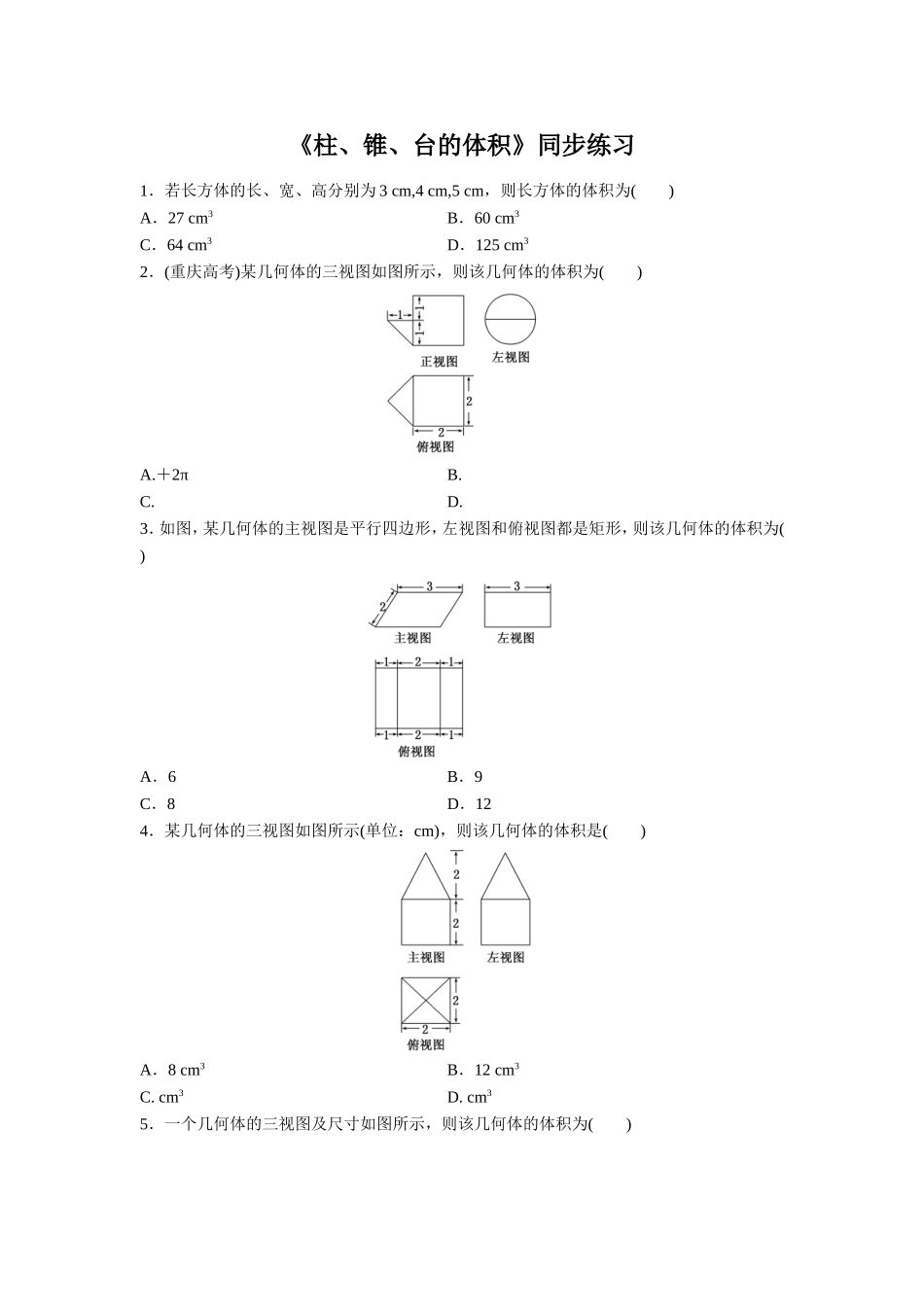
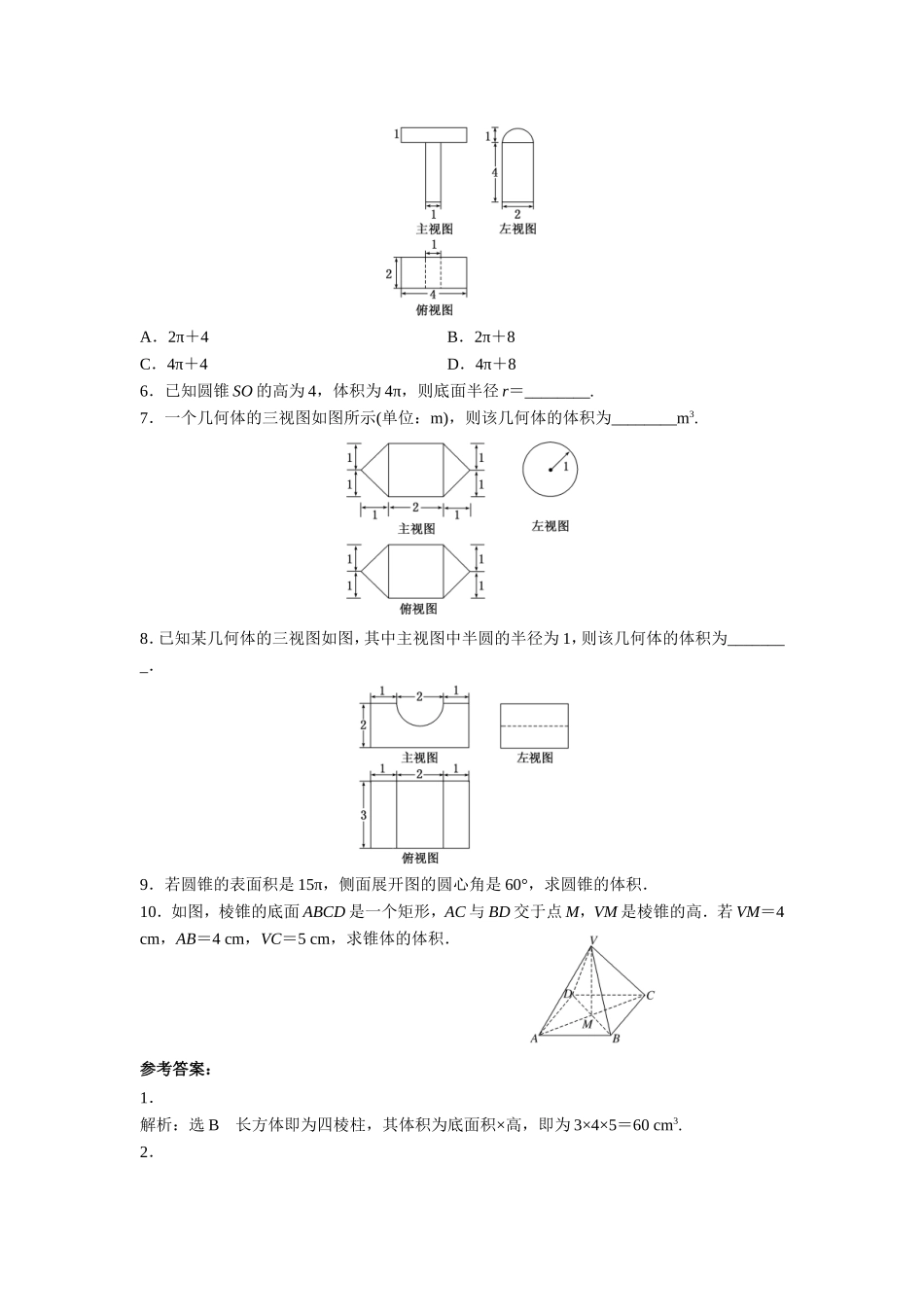
《柱、锥、台的体积》同步练习1.若长方体的长、宽、高分别为3cm,4cm,5cm,则长方体的体积为()A.27cm3B.60cm3C.64cm3D.125cm32.(重庆高考)某几何体的三视图如图所示,则该几何体的体积为()A.+2πB.C.D.3.如图,某几何体的主视图是平行四边形,左视图和俯视图都是矩形,则该几何体的体积为()A.6B.9C.8D.124.某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A.8cm3B.12cm3C.cm3D.cm35.一个几何体的三视图及尺寸如图所示,则该几何体的体积为()A.2π+4B.2π+8C.4π+4D.4π+86.已知圆锥SO的高为4,体积为4π,则底面半径r=________.7.一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.8.已知某几何体的三视图如图,其中主视图中半圆的半径为1,则该几何体的体积为________.9.若圆锥的表面积是15π,侧面展开图的圆心角是60°,求圆锥的体积.10.如图,棱锥的底面ABCD是一个矩形,AC与BD交于点M,VM是棱锥的高.若VM=4cm,AB=4cm,VC=5cm,求锥体的体积.参考答案:1.解析:选B长方体即为四棱柱,其体积为底面积×高,即为3×4×5=60cm3.2.解析:选B由三视图可知,该几何体是一个圆柱和半个圆锥组合而成的几何体,其体积为π×12×2+×π×12×1=π.3.解析:选B由三视图可知直观图是四棱柱,故V=×3×3=9.4.解析:选C由三视图可知,该几何体是由一个正方体和一个正四棱锥构成的组合体.下面是棱长为2cm的正方体,体积V1=2×2×2=8(cm3);上面是底面边长为2cm,高为2cm的正四棱锥,体积V2=×2×2×2=(cm3),所以该几何体的体积V=V1+V2=(cm3).5.解析:选B由三视图知该几何体的上面是一个半圆柱,下面是一个长方体,则由三视图的尺寸知该几何体的体积为V=1×2×4+×π×12×4=8+2π.6.解析:设底面半径为r,则πr2×4=4π,解得r=,即底面半径为.答案:7.解析:由几何体的三视图可知该几何体由两个圆锥和一个圆柱构成,其中圆锥的底面半径和高均为1,圆柱的底面半径为1且其高为2,故所求几何体的体积为V=π×12×1×2+π×12×2=π.答案:π8.解析:该几何体是一个长方体挖去一个半圆柱体,其体积等于3×2×4-3××π×12=24-.答案:24-9.解:设圆锥的底面半径为r,母线为l,则2πr=πl,得l=6r.又S锥=πr2+πr·6r=7πr2=15π,得r=,圆锥的高h=·,V=πr2h=π×××=π.10.解:∵VM是棱锥的高,∴VM⊥MC.在Rt△VMC中,MC===3(cm),∴AC=2MC=6(cm).在Rt△ABC中,BC===2(cm).S底=AB·BC=4×2=8(cm2),∴V锥=S底h=×8×4=(cm3).∴棱锥的体积为cm3.