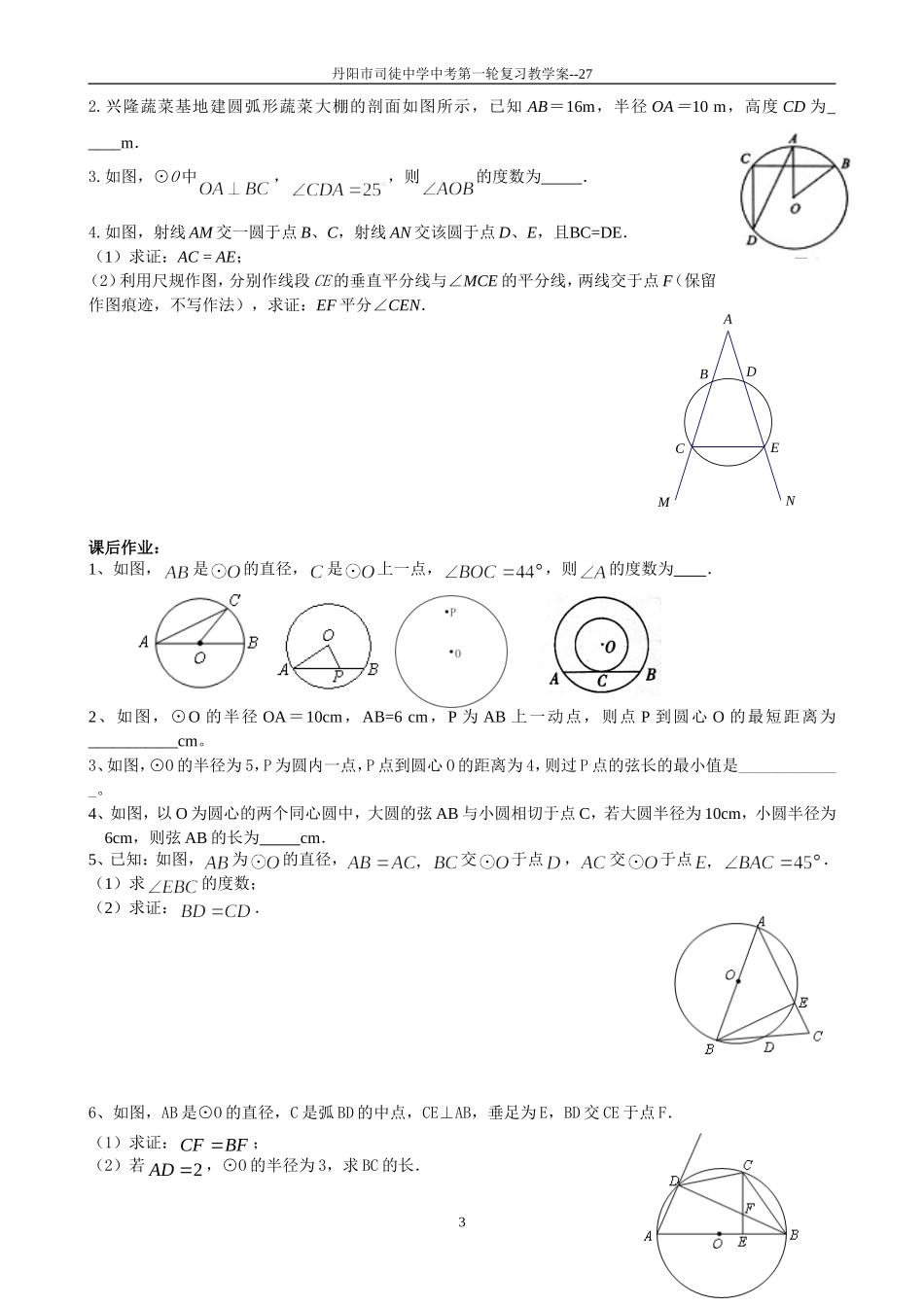
丹阳市司徒中学中考第一轮复习教学案--27课时27圆的有关概念与性质【基础知识】1.圆的定义:2.弦:3.弧:4.弦心距:5.圆心角:6.圆周角:7.圆内接多边形:8.圆是对称图形,任何一条直径所在的直线都是它的;圆又是对称图形,是它的对称中心.9.垂径定理:垂直于弦的直径平分,并且平分;平分弦(不是直径)的垂直于弦,并且平分.10.圆心角、弧、弦之间的关系:在同圆或等圆中,如果两个圆心角,两条弧,两条弦,两条弦心距,两个圆周角中有一组量,那么它们所对应的其余各组量都分别.11.圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角,都等于该弧所对的圆心角的。推论:直径所对的圆周角是,90°的圆周角所对的的弦是。12.圆内接四边形的性质:圆内接四边形的对角。13.三角形的内心、外心:(1)确定圆的条件:过的三点确定一个圆。(2)三角形的外心:(3)三角形的内心:14.(1)点与圆的的位置关系:①②③(2)直线与圆的位置关系:①②③15.切线判定定理:经过的外端,并且的直线是圆的切线。切线定理:圆的切线的半径。16.切线长定义:切线长定理:过圆外一点所画的圆的两条切线长。17.弧长:扇形面积:圆锥的侧面积:【知识应用】1.如图,是⊙O的直径,点在⊙O上,则的度数为________2.如图,已知圆心角,则圆周角的度数是_________3.如图所示,圆O的弦AB垂直平分半径OC.则四边形OACB的形状是_________4.如图,是⊙O的弦,于点,若,,则⊙O的半径为cm.5.如图,半圆的直径AB=___.6.已知:如图,,在射线AC上顺次截取AD=3cm,DB=10cm,1ACBO第4题第5题012-1-21AB第2题第1题第3题第1题丹阳市司徒中学中考第一轮复习教学案--27以DB为直径作⊙O交射线AP于E、F两点,求圆心O到AP的距离及EF的长.【例题讲解】例1如图:AC=CB,分别是半径和的中点,与的大小有什么关系?为什么?例2如图,AB为圆O的直径,CD⊥AB于点E,交圆O于点D,OF⊥AC于点F,(1)请写出三条与BC有关的正确结论。(2)当∠D=30°,BC=1时,求图中阴影部分的面积。例3已知:如图,在半径为4的⊙O中,AB,CD是两条直径,M为OB的中点,CM的延长线交⊙O于点E,且EM>MC.连结DE,DE=15.(1)求证:AMMBEMMC;(2)求EM的长;(3)求sin∠EOB的值.三、质疑反馈:1.下列命题中,正确的是()①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等A.①②③B.③④⑤C.①②⑤D.②④⑤2CBOEDAOFEDBCAABCEDOMBAOCD丹阳市司徒中学中考第一轮复习教学案--272.兴隆蔬菜基地建圆弧形蔬菜大棚的剖面如图所示,已知AB=16m,半径OA=10m,高度CD为_____m.3.如图,⊙O中,,则的度数为.4.如图,射线AM交一圆于点B、C,射线AN交该圆于点D、E,且BC=DE.(1)求证:AC=AE;(2)利用尺规作图,分别作线段CE的垂直平分线与∠MCE的平分线,两线交于点F(保留作图痕迹,不写作法),求证:EF平分∠CEN.课后作业:1、如图,是的直径,是上一点,,则的度数为.2、如图,⊙O的半径OA=10cm,AB=6cm,P为AB上一动点,则点P到圆心O的最短距离为___________cm。3、如图,⊙O的半径为5,P为圆内一点,P点到圆心O的距离为4,则过P点的弦长的最小值是_____________。4、如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,则弦AB的长为cm.5、已知:如图,为的直径,交于点,交于点.(1)求的度数;(2)求证:.6、如图,AB是⊙O的直径,C是弧BD的中点,CE⊥AB,垂足为E,BD交CE于点F.(1)求证:CFBF;(2)若2AD,⊙O的半径为3,求BC的长.3ABCDEMN丹阳市司徒中学中考第一轮复习教学案--277、如图,在边长为2的圆内接正方形ABCD中,AC是对角线,P为边CD的中点,延长AP交圆于点E.(1)∠E=度;(2)写出图中现有的一对不全等的相似三角形,并说明理由;(3)求弦DE的长.8、如图,已知在⊙O中,AB=4,AC是⊙O的直径,AC⊥BD于点F,∠A=30°.(1)求图中阴影部分的面积;(2)若用阴影扇形OBD围成一个圆锥侧面,请求出这个圆锥的底面圆的半径.9、如图,在扇形OAB中,∠AOB=90°,半径OA=6.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上的点D处,折痕交OA于点C,求整个阴影部分的周长和面积.4