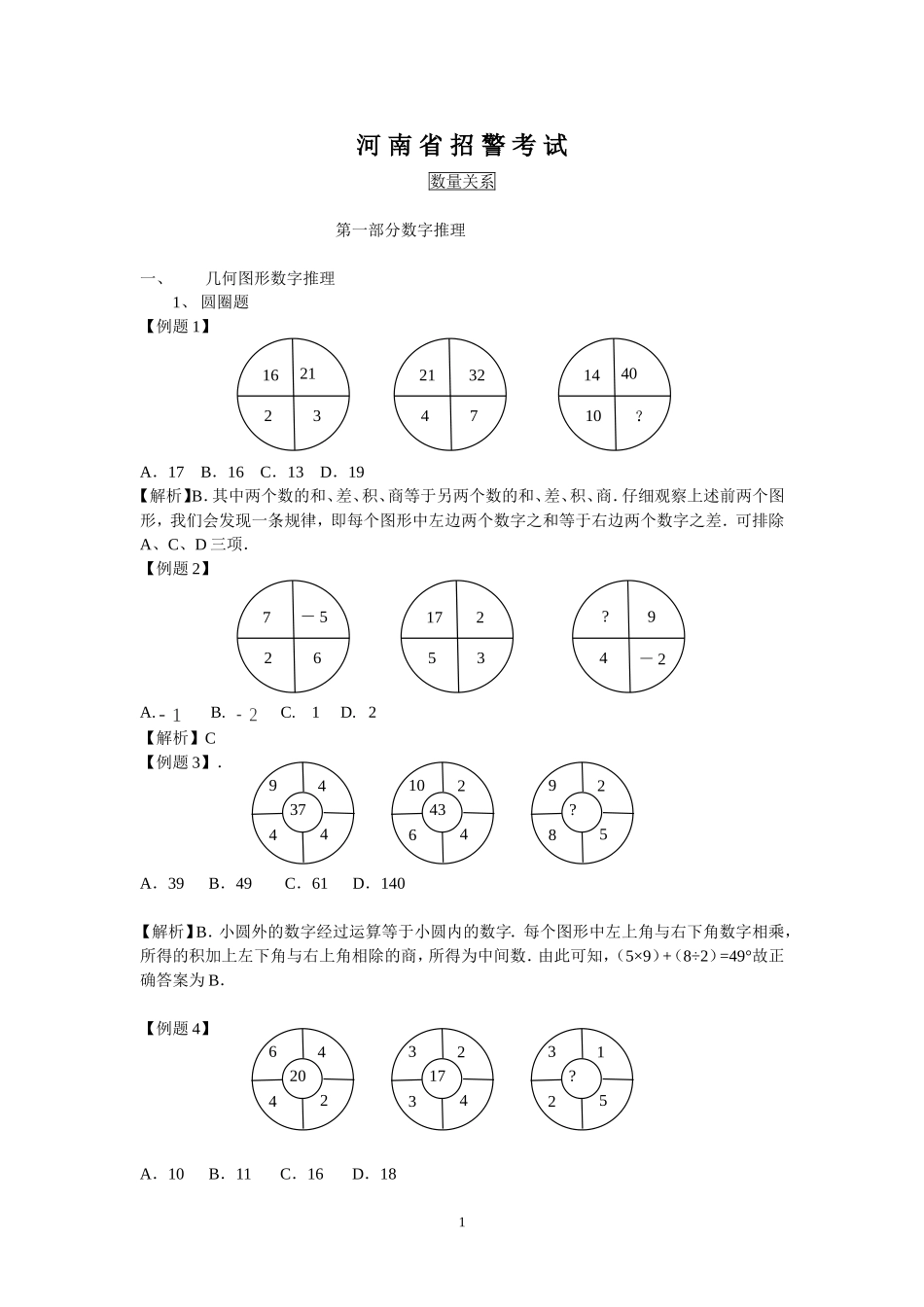
河南省招警考试数量关系第一部分数字推理一、几何图形数字推理1、圆圈题【例题1】A.17B.16C.13D.19【解析】B.其中两个数的和、差、积、商等于另两个数的和、差、积、商.仔细观察上述前两个图形,我们会发现一条规律,即每个图形中左边两个数字之和等于右边两个数字之差.可排除A、C、D三项.【例题2】A.B.C.1D.2【解析】C【例题3】.A.39B.49C.61D.140【解析】B.小圆外的数字经过运算等于小圆内的数字.每个图形中左上角与右下角数字相乘,所得的积加上左下角与右上角相除的商,所得为中间数.由此可知,(5×9)+(8÷2)=49°故正确答案为B.【例题4】A.10B.11C.16D.181294374492?58102434632517?94-26-527?40101432121673242164202431?52321743【解析】D.规律:每个图形中左上角的数字乘以右下角的数字再加上另外两个数字正好等于中间所求数字,根据规律可知问号处数字应为:3×5+1+2=18°据此,可排除A、B、C三项.2.九宫格.【例题5】126?6820141240A.6B.10C.20D.30【解析】D.2×前项+中项=后项。【例题6】305648?1272324A.2B.4C.8D.12【解析】B.前项=中项×后项。【例题7】654612126?8A.6B.7C.8D.10【解析】D.第三行数字=第一行数字×第二行数字/6。二、常见题型第一种题型:等差数列1、基础等差数列【拓展延伸】后一项减前一项等于一个常数.各项数值均匀递增或递减,数值变化幅度相同.【例题1】13,24,35,(),57A.46B.49C.52D.56【解析】答案为A常用的等差数列有:自然数列1,2,3,4,5,6,奇数数列1,3,5,7,9,偶数数列2,4,6,8,10,2、二级等差数列【拓展延伸】一个数列相邻两项两两做差,得到一个等差数列.数列各项数值依次递增或递减,变化幅度逐渐变大或变小,但总体上各项数值起伏较为缓和,需要做差两次.2【例题1】5,8,14,23,(),50A.34B.30C.35D.45【解析】答案为C【例题2】32,27,23,20,18,()A.14B.15C.16D.17【解析】答案为D【例题3】0,8,24,48,80,()A.120B.116C.108D.100【解析】答案为A3、二级等差数列的变式【拓展延伸】数列后一项减前一项所得的新数列是一个基础数列,可能是自然数列,等比数列,平方数列,立方数列或者与这些数列加减“1”、“2”的形式有关°数列特点:数列各项变化幅度较大.【例题1】25,27,30,35,42,()A.60B.55C.53D.48【解析】答案C二级为质数列2,3,5,7,11,【例题2】2,3,7,16,(),57A.25B.29C.32D.41【解析】答案为C二级为平方数列1,4,9,16,25,【例题3】1,4,8,14,24,42,()A.80B.76C.70D.48【解析】答案B二级特征不明显,三级为公比为2的等比数列.【练习】【题1】2,6,14,30,()A.30B.38C.44D.62【题2】11,12,15,20,27,()A.32B.34C.36D.3【题3】1,8,21,40,(),96A.55B.60C.65D.70【题4】1,4,8,13,16,20,()A.20B.25C.27D.28【题5】5,12,21,34,53,80,()A.121B.115C.119D.117【答案与解析】【题1】D二级为公比为2的等比数列.【题2】C二级为公差为2的等差数列.【题3】C二级为公差为6的等差数列,对于未知相在中间的多级数列,需要我们采用先“猜”后“验”的方法.【题4】B二级为周期数列.【题5】D三级等差数列.第二种题型:等比数列1、等比数列【拓展延伸】数列相邻两项两两做商,商为同一个常数.数列形式特点:数列各项均为倍数关3系,各项数值变化幅度较大.【例题1】2,6,18,54,162,()A.164B.168C.328D.486【解析】答案为D2、二级等比数列【拓展延伸】相邻两项两两做差(或商),得到一个等比数列.【例题2】1,3,18,216,(),A.432B.1024C.5184D.6125【解析】答案C做商,二级是公比为2的等比数列,3,6,12,24,故未知项应为216×24=5184【例题3】8,6,2,-6,()A.-8B.-10C.-20D.-22【解析】答案D做差,二级是公比为2的等比数列.【注释】本题前一项的2倍减去10等于后一项.【例题4】32,48,40,44,42,()A.43B.45C.47D.49【解析】答案A做一次差,二级是公比为的等比数列.【注释】从第三个数开...