高等光学课件chap4.1VIP免费

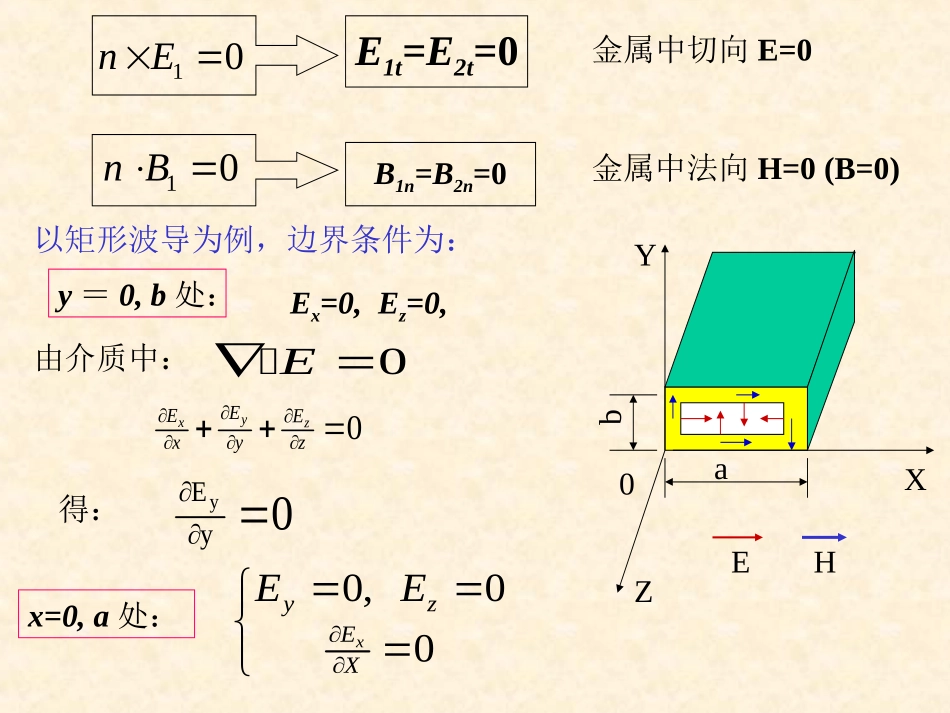
波导管中的场方程为亥姆霍兹方程022EKE电磁波在介质中传播无衰减电磁波可分解为谐波，沿Z方向传播波导管壁是理想管壁1波导内0波导媒介中00ZXYab波导管中的场方程电磁波在金属波导中传播电磁波在金属波导中传播(microwav(microwave)e)以矩形波导为例，边界条件为：0yEyx=0,a处：0,00xyzEXEE0E由介质中：得：y＝0,b处：Ex=0,Ez=0,B1n=B2n=0E1t=E2t=010nE10nB金属中切向E=0金属中法向H=0(B=0)0ZXYabEH0yxzEEExyzEHxy0abEyEyExExHxHxHyHyx=0,a处：0,00xyzEXEE0,00yxzEYEEy＝0,b处：电力线垂直导体表面，磁力线切于导体表面一般形式的边界条件0En0Bn0nEnnEBn电力线垂直导体表面，磁力线切于导体表面E——的切向分量连续金属中E=0B——的法向分量连续金属中H=0(B=0)0E亥姆霍兹方程的一般求解亥姆霍兹方程的一般求解(,,,)(,)zikzitExyztExyee()(,)zikzErExye022EKE0),()(),()(222222yxEKKyxEzyx采用分离变量法，设：设：)()(),(yYxXyxu通解其中可以是uxyExyExyExyxyz(,):(,),(,),(,)代入亥姆霍兹方程，分离X,Y得:22222200dXxdxdYydyKXKY1122(,)[cos()sin()][cos()sin()]xxyyUxyCKxDKxCKyDKy1122cos()sin()cos()sin()xxyyXCKxDKxYCKyDKy通解通解：)()(),(yYxXyxu)()(),(yYxXyxu通解将：各个方程通解为：利用边界条件来求特解利用边界条件来求特解0,0,0,:0,00,:0,0xyyzExxaxxzEyybyxaEEybEE对于Ex分量：0,000yxxxEEx0)sincos(cos)sincos)(cossin(0221022110xyyxxxyyxxxxxxEyKDyKCxKKDyKDyKCxKKDxKKCx对于任意y均成立D1=0x＝0,y＝0的情况)yKsinDyKcosC)(xKsinDxKcosC()y,x(Uy2y2x1x1由xy0abEyEyExExHxHxHyHy边界条件同理对于Ey、Ez作类似计算，得123cos()sin()sin()cos()sin()sin()zzziKzxxyiKzyxyiKzzxyEAKxKyeEAKxKyeEAKxKye012(cos)(cos)0xyxyECKxCKy同理由C2=0122(,)(cos)(cossin)xyyUxyCKxCKyDKy根据D1=0对任意x都成立，必须)yKsinDyKcosC)(xKsinDxKcosC()y,x(Uy2y2x1x1由注：为何不能C1＝0？若C1＝0，代入通解后U＝0全部没有了。(,,,)()itxyzExyztEEEex=a,y=bx=a,y=b的两个界面上的边界条件的两个界面上的边界条件0sinsin)sincos(011axyxxaxyxxaxxExyKxKKAyKxKA1cos()sin()xxyEAKxKyx=a时，Ey=Ez=0对于任意y都成立0,1,2m/a0sinmKaKxx0,1,2n/bnKy同理有1a2a3acos()sin()sin()cos()sin()sin()zzziKzmnxbiKzmnybiKzmnzbEAxyeEAxyeEAxye()00xyzxyzxyzEEEEE代入，可得0321AiKAKAKzyx该式表明A1，A2，A3中只有二个独立。表明E1，E2，E3中只有二个独立二个独立模式几点讨几点讨论论1、模式m、n只能取正整数，是离散的，所以有不同的场分布结构，即模式，如TEmn、TMmn模。通常：1：Ez=0电场在Z方向上无分量—>横电波TE波2：Hz=0磁场在Z方向上无分量—>横磁波TM波2、横向振荡特性E及H各分量沿横坐标(x,y)分布是驻波分布m是正整数，表示沿波导的a（x方向）上分布的驻波个数(半波的数目)，n为b方向的驻波个数(半波的数目)。1cos()sin()ziKzmnxabEAxye例如：•1)、矩形波导中不可能存在TE00,TM00波（各分量不同时为零）。•2)、矩形波导中不可能存在TEM波。（Kx、Ky不同时为零，Ez、Hz不同时为零）,0,(),zyyxxxzyiHEEEEEEiiiHHHzxyz3、截止频率所谓的截止频率指的是：当电磁波频率低于某个定值时就不能在给定的波导内传播。)(2222yxzKKKK为相位，可以传播。传播因子为实数（取正）时，当KZyxKKK)(222成为衰减，无法传播。为虚数，时，时，可以传播。当cKKcyxcKKKKK,22221221,...