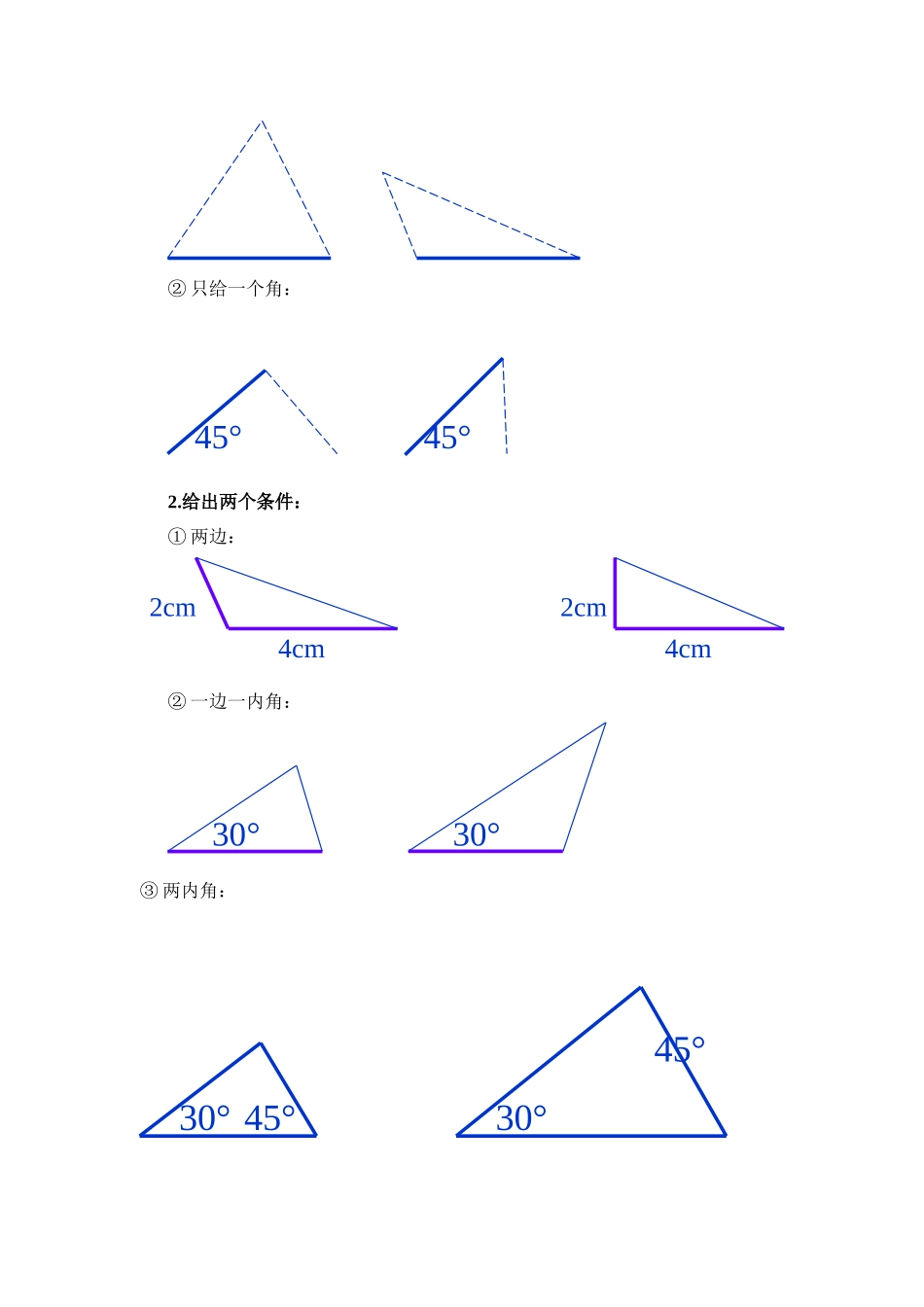
《12.2全等三角形的判定》横峰二中王爱云教学目标1.知识目标:掌握“边边边”条件的内容,并能初步应用“边边边”条件判定两个三角形全等.2.能力目标:使学生经历探索三角形全等条件的过程,体会如何探索研究问题,并初步体会分类思想,提高学生分析问题和解决问题的能力.3.思想目标:通过画图、比较、验证,培养学生注重观察、善于思考、不断总结的良好思维习惯。教学重点、难点重点:利用边边边证明两个三角形全等难点:探究三角形全等的条件教学过程(一)复习提问1.什么叫全等三角形?2.全等三角形有什么性质?3.若△ABC≌△DEF,点A与点D,点B与点E是对应点,试写出其中相等的线段和角.(二)新课讲解问题1:在△ABC和△DEF中,AB=DE,BC=EF,AC=DF,∠A=∠D,∠B=∠E,∠C=∠F,则△ABC和△DEF全等吗?问题2:△ABC和△DEF全等是不是一定要满足AB=DE,BC=EF,AC=DF,∠A=∠D,∠B=∠E,∠C=∠F这六个条件呢?若满足这六个条件中的一个、两个或三个条件,这两个三角形全等吗?探究一:1.只给一个条件(一组对应边相等或一组对应角相等)。①只给一条边:②只给一个角:2.给出两个条件:①两边:②一边一内角:③两内角:45°45°2cm2cm4cm4cm30°30°30°30°45°45°问题3:两个三角形若满足这六个条件中的三个条件能保证它们全等吗?满足三个条件有几种情形呢?3.给出三个条件三个条件可分为:三个角相等、三条边相等、两角一边相等、两边一角相等例:画△ABC,使AB=5cm,AC=4cm,BC=8cm画法:1画线段BC=6cm2分别以B、C为圆心,以5cm和4cm为半径作弧,交于点A。则△ABC即为所求的三角形把你画的三角形与其同桌所画的三角形剪下来,进行比较,它们能否互相重合?归纳:有三边对应相等的两个三角形全等.可以简写成“边边边”或“SSS”用数学语言表述:在△ABC和△DEF中AB=DEBC=EFCA=FD∴△ABC≌△DEF(SSS)(三)题例训练:例1.如下图,△ABC是一个刚架,AB=AC,AD是连接A与BC中点D的支架。求证:△ABD≌△ACD证明:∵D是BC中点BD=CD在△ABD和△ACD中:AB=AC(已知)AD=AD(公共边)ABCDBD=CD(已证)∴△ABD≌△ACD(SSS)(如果题目改为,求证:∠B=∠C呢?)证明的书写步骤:①准备条件:证全等时把要用的条件要先证好;②三角形全等书写步骤:1写出在哪两个三角形中2摆出三个条件用大括号括起来3写出全等结论例2:如图,在四边形ABCD中,AB=CD,AD=BC,求证:△ABC≌△CDA证明:在△ABC和△CDA中AB=CD(已知)AD=BC(已知)AC=AC(公共边)∴△ABC≌△CDA(SSS)变式一:已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=FB(如图),能证明△ABC≌△FDE吗?(由学生完成)变式二:已知:如图,AB=AC,DB=DC,请说明∠B=C∠成立的理由(由学生完成)(四)课堂小结:通过这节课的学习,你有什么收获?AABBCCDD(五)布置作业:《作业本》1课时。