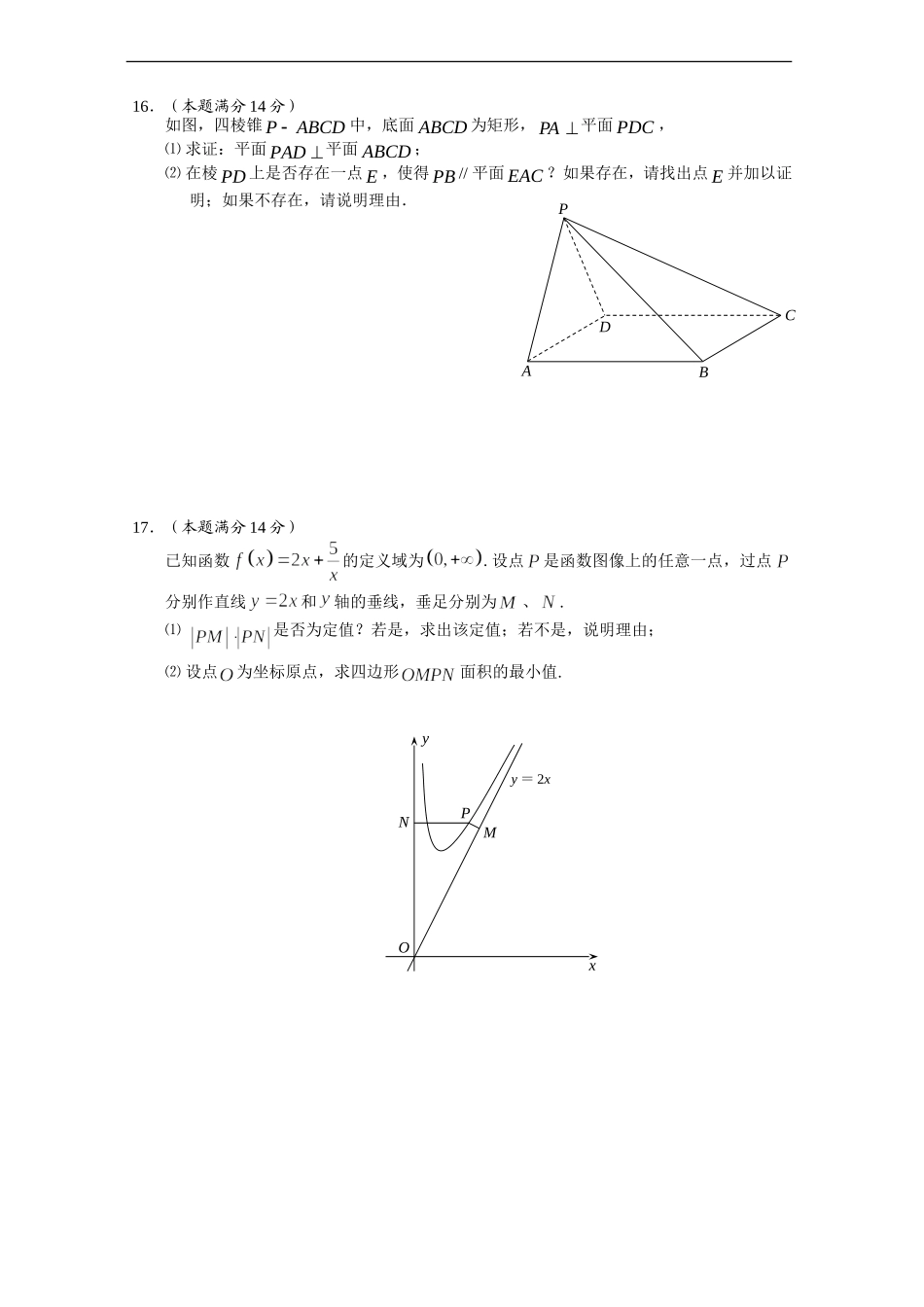
2014届第一学期期中考试高三文科数学试题一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上)1.已知集合},12,3,1{,,32mBmA若BA,则实数m的值为▲.2.函数的最小正周期是▲.3.已知两条直线12:330,:4610.laxylxy若12//ll,则a▲.4.已知等差数列}{na的前n项和为nS,若,则7S的值为▲.5.已知向量,,.若向量与向量共线,则实数k▲.6.已知直线l平面,直线m平面,给出下列命题:①若//,则lm;②若,则//lm;③若//lm,则;④若lm,则//.其中正确命题的序号是▲.(把所有正确的命题序号都填上)7.定义在R上的函数()fx满足:,且,则=▲.8.若实数x,y满足,则的最大值是▲.9.在直角三角形ABC中,90ACB,2ACBC,点P是斜边AB上的一个三等分点,则CPCBCPCA�▲.10.已知函数,其中π[,]6xa.若()fx的值域是,则a的取值范围2013.11是▲.11.如图,在正三棱锥A-BCD中,底面正三角形的边长为2,点E是AB的中点,AC⊥DE,则正三棱锥A-BCD的体积是▲.12.已知点P的坐标,过点P的直线l与圆相交于A、B两点,则的最小值为.13.定义域为R的函数,若关于x的方程恰有5个不同的实数解,,,,,则等于▲.14.曲线C:)0,0(||baaxby与y轴的交点关于原点的对称点称为“望点”,以“望点”为圆心,凡是与曲线C有公共点的圆,皆称之为“望圆”,则当时,所有的“望圆”中,面积最小的“望圆”的面积为▲.二、解答题:(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)15.(本题满分14分)在中,角所对的边分别为,且.⑴求函数的最大值;⑵若,求c的值.EBDCA16.(本题满分14分)如图,四棱锥ABCDP中,底面ABCD为矩形,PA平面PDC,⑴求证:平面PAD平面ABCD;⑵在棱PD上是否存在一点E,使得PB//平面EAC?如果存在,请找出点E并加以证明;如果不存在,请说明理由.17.(本题满分14分)已知函数的定义域为.设点是函数图像上的任意一点,过点分别作直线和轴的垂线,垂足分别为、.⑴是否为定值?若是,求出该定值;若不是,说明理由;⑵设点为坐标原点,求四边形面积的最小值.DPABCyxNOPMy=2x18.(本题满分16分)甲乙两地相距300千米,一汽车从甲地匀速行驶到乙地,速度不得超过a千米/小时,已知该汽车每小时的运输成本P(元)关于速度(千米/小时)的函数关系是.⑴试将全程运输成本(元)表示为速度的函数;⑵为使全程运输成本最少,汽车应以多少速度行驶?并求此时运输成本的最小值.19.(本题满分16分)已知数列中,,,数列满足.⑴求证数列是等差数列,并求数列的通项公式;⑵求数列的前项和;⑶设数列满足(为非零常数,),问是否存在整数,使得对任意,都有.20.(本题满分16分)已知函数.⑴若,求曲线在点处的切线方程;⑵若,求函数的单调区间;⑶设函数.若至少存在一个,使得成立,求实数的取值范围.2014届第一学期期中考试ADBCPOEAPCBD高三文科数学试题答案一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卡相应的位置上)1、12、3、24、215、16、①③7、8、9、410、11、12、13、214、二、解答题:(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)15.(本题满分14分)解:(1).……3分因为,所以.………………4分则所以当,即时,取得最大值,且最大值为.………7分(2)由题意知,所以.又知,所以,则.………………10分因为,所以,则.………………12分由得,.………………14分16.(本题满分14分)2013.11(1)证明:PA平面PDC,平面PDC,CDPA.………………2分四边形ABCD为矩形,CDAD,………………4分,CD平面PAD.………………6分平面ABCD平面PAD平面ABCD.………………7分(2)答:当点E为棱PD中点时,PB//平面EAC.………………9分证明:取棱PD中点E,连接BD与AC相交于点O,连结EO.四边形ABCD为矩形,O为BD中点.E为棱PD中点.EOPB//.………………12分PB平面EAC,EO平面EAC,直线PB//平面EAC.………………14分17.(本题满分14分)解:...