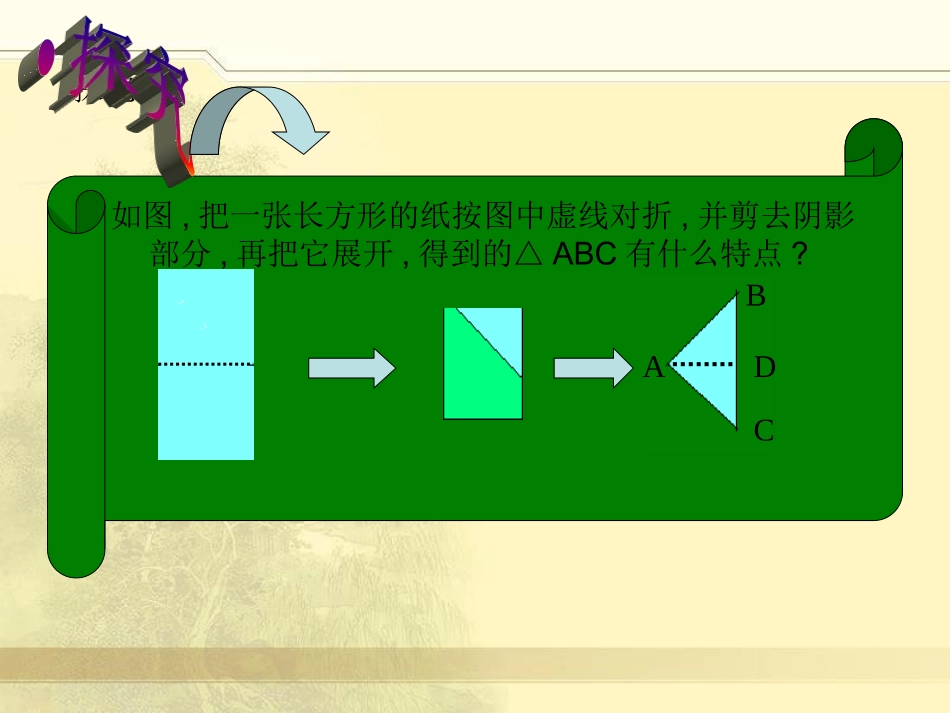
13.3等腰三角形1如图,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC有什么特点?探究BACD13.3等腰三角形ABC等腰三角形:有两边相等的三角形几何符号语言:△ABC中,AB=AC腰腰底边顶角底角底角345678910把剪出的等腰三角形ABC沿折痕对折,你能发现什么现象?11②∠B=∠C两个底角相等③BD=CDAD为底边BC上的中线④∠BAD=∠CADAD为顶角∠BAC的平分线⑤∠ADB=∠ADC=90°AD为底边BC上的高①折叠的两部分互相重合是轴对称图形现象结论ABCD12等腰三角形的性质:性质1等腰三角形的两个底角相等性质2等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合(等边对等角);(三线合一)。几何符号语言:∵AB=AC∴∠B=∠C13如何用所学的知识验证等腰三角形的性质1?14证明:作顶角的平分线AD.在△BAD和△CAD中,AB=AC∠1=2∠AD=AD△△BAD△CAD(SAS).△∴∠B=C∠已知:△ABC中,AB=AC.求证:∠B=∠C.ABC12D你还能用其他方法证明吗?15已知:如图,在△ABC中,AB=AC,AD是底边BC上的中线求证:∠BAD=∠CAD,AD⊥BCABCD16等腰三角形“三线合一”性质用几何符号语言表示为:(1)∵AB=AC,AD平分∠BAC∴________⊥_______,______=_______(2)∵AB=AC,AD⊥BC,∴∠_____=∠____,______=_______(3)∵AB=AC,BD=CD,∴∠_____=∠____,________⊥_______,ADBCBDCDBADCADBDCDBADCADADBCABCD17例1如图:在△ABC中,AB=AC,点D在AC上,且BD=BC=AD,求△ABC各角的度数。∵AB=AC,解:∴∠A=∠ABD设∠A=x,则∠BDC=∠A+∠ABD=2x,从而∠ABC=∠C=∠BDC=2x,∵∠A+∠ABC+∠C=180°,解得x=36°∴在△ABC中,∠A=36°,∠ABC=∠C=72°。ABCD∵BD=BC∴∠C=∠BDC∴∠ABC=∠C∴∠ABC=∠C=∠BDC∵BD=AD则∠ABD=x即:x+2x+2x=180°18⒈等腰三角形一个底角为70°,则其余两角为______.⒉等腰三角形一个角为70°,则其余两角为__________________.⒊等腰三角形一个角为110°,则其余两角为___________.70°,40°35°,35°70°,40°或55°,55°19如图:△ABC是等腰直角三角形,AB=AC,∠BAC=90°,AD是底边BC上的高,求∠B、∠C、∠BAD、∠DAC的度数。ABCD20怎样的三角形叫做等腰三角形?有______________的三角形叫做_______________。ABC腰腰底边顶角底角底角思考两条边相等等腰三角形等腰三角形的性质:等腰三角形的两个底角相等(等边对等角)21ABCD如图:在三角形ABC中,AB=AC,且AD=BD,请大家数一数,这个图形中一共有多少个等腰三角形?△ABC(AB=AC),△ADB(AD=BD)若将条件改为AD=BD=BC,则有多少个等腰三角形?△ABC(AB=AC)△ADB(AD=BD)△BDC(BD=BC)22等腰三角形等腰三角形的性质的性质1等腰三角形的两个底角相等(等边对等角)例1在三角形ABC中,已知AB=AC,且∠B=80°,则∠C=——度,∠A=——度?∵AB=AC(已知)∴∠B=C∠(等边对等角)∵∠B=80°(已知)∴∠C=80°又∵∠A+B+C=180°∠∠(三角形内角和为180°)∴∠A=180°-∠B-∠C∠A=20°BCA23操练操练11在三角形ABC中,已知AB=AC,且∠A=50°,则∠B=——度,∠C=——度?CBA∵AB=AC(已知)∴∠B=C∠(等边对等角)又∵∠A+B+C=180°∠∠(三角形内角和为180°)∠A=50°(已知)∴∠B=65°∠C=65°等腰三角形等腰三角形的性质的性质1等腰三角形的两个底角相等(等边对等角)24操练操练22在等腰三角形ABC中,如果AB=AC,且一个角等于70°,求另两个角的度数。若顶角即∠A=70°则∠B=55°C=55°∠若底角即∠B=70°则∠C=70°A=40°∠若底角即∠C=70°则∠B=70°A=40°∠在等腰三角形中,我们只要知道任一个角,就可以求出另外两个角!CBA若改为90°呢?等腰三角形等腰三角形的性质的性质1等腰三角形的两个底角相等(等边对等角)25ABCD例1如图:在△ABC中,AB=AC,点D在AC上,且BC=AD=BD,求△ABC各角的度数。解:∵AB=AC,BC=AD=BD)∴∠ABC=C=BDC∠∠∠A=ABD∠(等边对等角)设∠A=x,则∠BDC=A+ABD=2X∠∠从而∠ABC=C=BDC=2X∠∠于是在△ABC中,有∠A+ABC+C=X+2X+2X=180∠∠0解得X=360在△ABC中,∠A=360,∠ABC=C=72∠026趣味数学:如图:点B、C、D、E、F在∠MAN的边上,∠A=15°,AB=BC=CD=DE=EF,求∠MEF的度数。ABCDEFMN27小结:本堂课主要学习了等腰三角形的性质:等边对等角。只要知道等腰三角形的一个角的度数,我们就可以求出另外两个角的度数!当这个角为锐角时,它可能是等腰三角形的顶角,也可能是等腰三角形的底角;当这个角为钝角时,它只能是等腰三角形的顶角。28