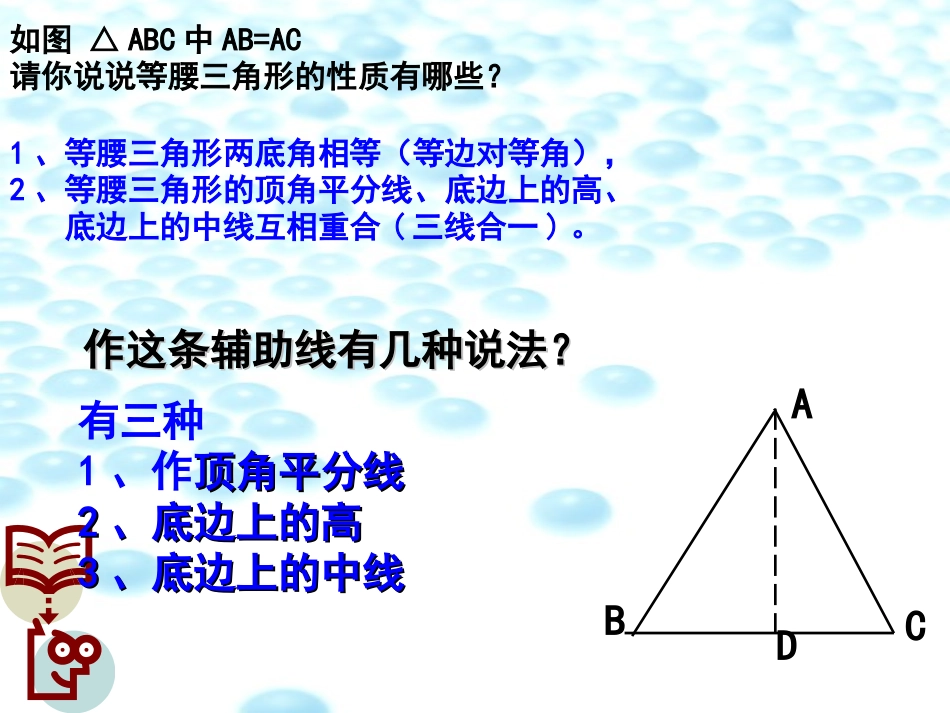
12.3.1等腰三角形(2)如图△ABC中AB=AC请你说说等腰三角形的性质有哪些?1、等腰三角形两底角相等(等边对等角),2、等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合(三线合一)。DCBA作这条辅助线有几种说法?作这条辅助线有几种说法?有三种1、作顶角平分线顶角平分线22、底边上的高、底边上的高33、底边上的中线、底边上的中线ABOO探索新知•如图位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?解:如图作AB边上的高OCC由∠∠ACO=∠∠BCO∠∠A=∠∠BOC=OC得△ACO≌△BCO(AAS)∴OA=OB从而肯定两艘救生船以同样的速度同时出发,两艘救生船以同样的速度同时出发,大约能同时赶到出事地点。大约能同时赶到出事地点。在一般的三角形中,如果有两个角相等,那么它们所对的边有什么关系?等腰三角形的判定:如果一个三角形中有两个角相等,那么这两个角所对的边也相等.(简称为:等角对等边)等腰三角形的性质与判定有区别吗?性质是:等边等角判定是:等角等边解:作ΔABC的角平分线AD,在在ΔABDΔABD和和ΔACDΔACD中中∠∠B=∠CB=∠C∠∠1=∠21=∠2AD=ADAD=AD(已知)(角平分线的意义)(公共边)∴∴ΔABD≌ΔACD(AAS)ΔABD≌ΔACD(AAS)∴∴AB=ACAB=AC如果一个三角形有两个角相等,那么这个三角形是等腰三角形。简单地说,在同一个三角形中,等角对等边。21DBCA(全等三角形的对应边相等)∴∴ΔABCΔABC是等腰三角形是等腰三角形例2求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。AECBD问题:1.如何将文字叙述的几何命题转化成几何语言?2.命题中条件和结论分别指出来?3.写出已知、求证。AECBD求证:AB=AC证明:∵AEBC∥AEBC∥(已知)(已知)∴∠1=B()∠∠2=C()∠∵AEAE是△是△ABCABC的外角平分线(已知)的外角平分线(已知)∠1=2∠(角平分线定义)∴∠B=C∠∴AB=AC()已知:已知:AEAE是△是△ABCABC的外角平的外角平分线分线,,且且AE∥BC.AE∥BC.两直线平行,同位角相等两直线平行,内错角相等等角对等边例2求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形。练习2、如图,把一张矩形的纸沿对角线折叠,重合的部分是一个等腰三角形吗?为什么?ABCGDE123解:重合部分是等腰三角形。理由:由ABDC是矩形知AC∥BD∴∠3=∠2由沿对角线折叠知∠1=∠2∴∠1=∠3∴BG=GC(等角对等边)名称图形概念性质与边角关系判定等腰三角形ABC有两边相等的三角形是等腰三角形2.等边对等角3.三线合一4.是轴对称图形2.等角对等边1.两边相等1.两腰相等小结