椭圆的参数方程课件VIP免费

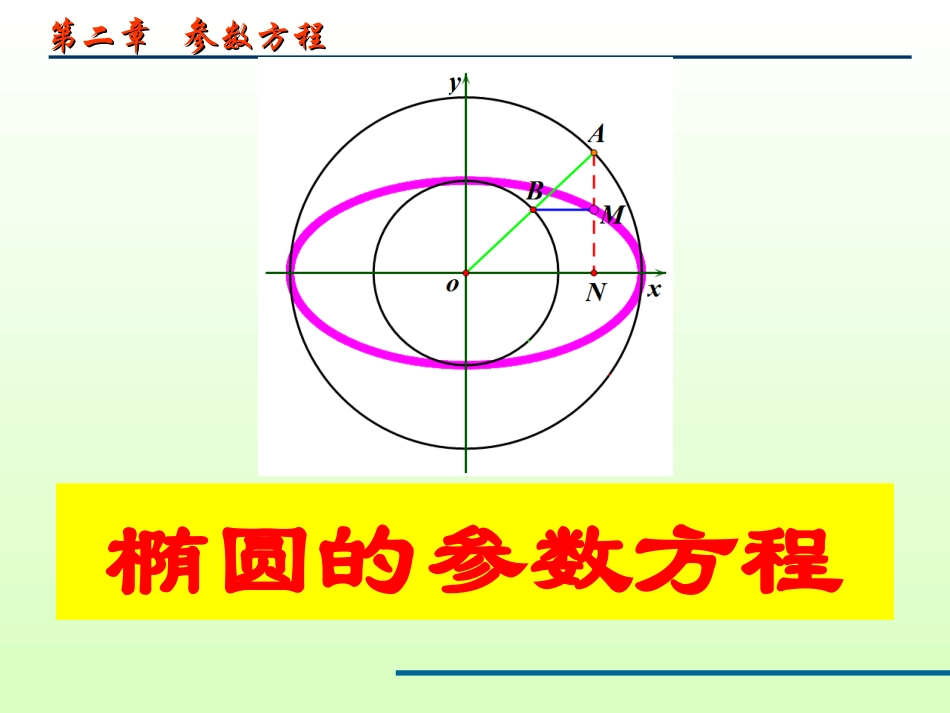
第二章参数方程第二章参数方程椭圆的参数方程1.圆心在原点,半径为r的圆的参数方程:为参数）(sincosryrx2.圆心为(a,b),半径为r的圆的参数方程:为参数）(sincosrbyrax圆的参数方程:温故知新美妙的参数曲线(.gsp)探究、如下图，以原点为圆心，分别以a，b（a＞b＞0）为半径作两个圆，点B是大圆半径OA与小圆的交点，过点A作AN⊥ox，垂足为N，过点B作BM⊥AN，垂足为M，求当半径OA绕点O旋转时点M的轨迹参数方程.分析：点M的横坐标与点A的横坐标相同,点M的纵坐标与点B的纵坐标相同.而A、B的坐标可以通过引进参数建立联系.xOA设xyMNBoA问题探究解：由已知:即为点Ｍ的轨迹参数方程.消去参数得:1,byax2222即为点Ｍ的轨迹普通方程.),(,yxMxOA设)sin,cos(:aaA)sin,cos(:bbB为参数）(sincosbyax1.参数方程是椭圆的参数方程.cosxasinyb2.在椭圆的参数方程中，常数a、b分别是椭圆的长半轴长和短半轴长.a>b>0一般，称为离心角,规定参数的取值范围是[0,2)cos,sin.xaXyb焦点在轴cos,sin.xbYya焦点在轴学有所得【练习】把下列普通方程化为参数方程.把下列参数方程化为普通方程即学即用1925)3(22yx110064)4(22yx149)1(22yx116)2(22yxsin2cos3)1(yxsin4cos)2(yxsin2cos3)1(yxsin3cos5)3(yxsin10cos8)4(yx典例分析例1：动点M(x,y)在曲线上变化。（1）求2x+3y的最大值和最小值.14922yx)cos()sin(cossin2222bababa辅助角公式：（2）求z=x-2y的最小值.椭圆的参数方程椭圆的标准方程：12222byax横sincosbyax横椭圆的参数方程：一般地：2,012222aybx纵sincosaybx纵在椭圆的参数方程中，常数a、b分别是椭圆的长半轴长和短半轴长.a>b课堂小结称为离心角，当堂测评导学案“当堂检测”课后作业模块测评（练习册）第38页例1、例2课堂延伸拓展：动点M(x,y)在曲线上变化。你有几种方法求点M到直线的距离的最小值？能用线性规划类似的方法吗？14922yx0102yx感谢各位专家莅临指导！