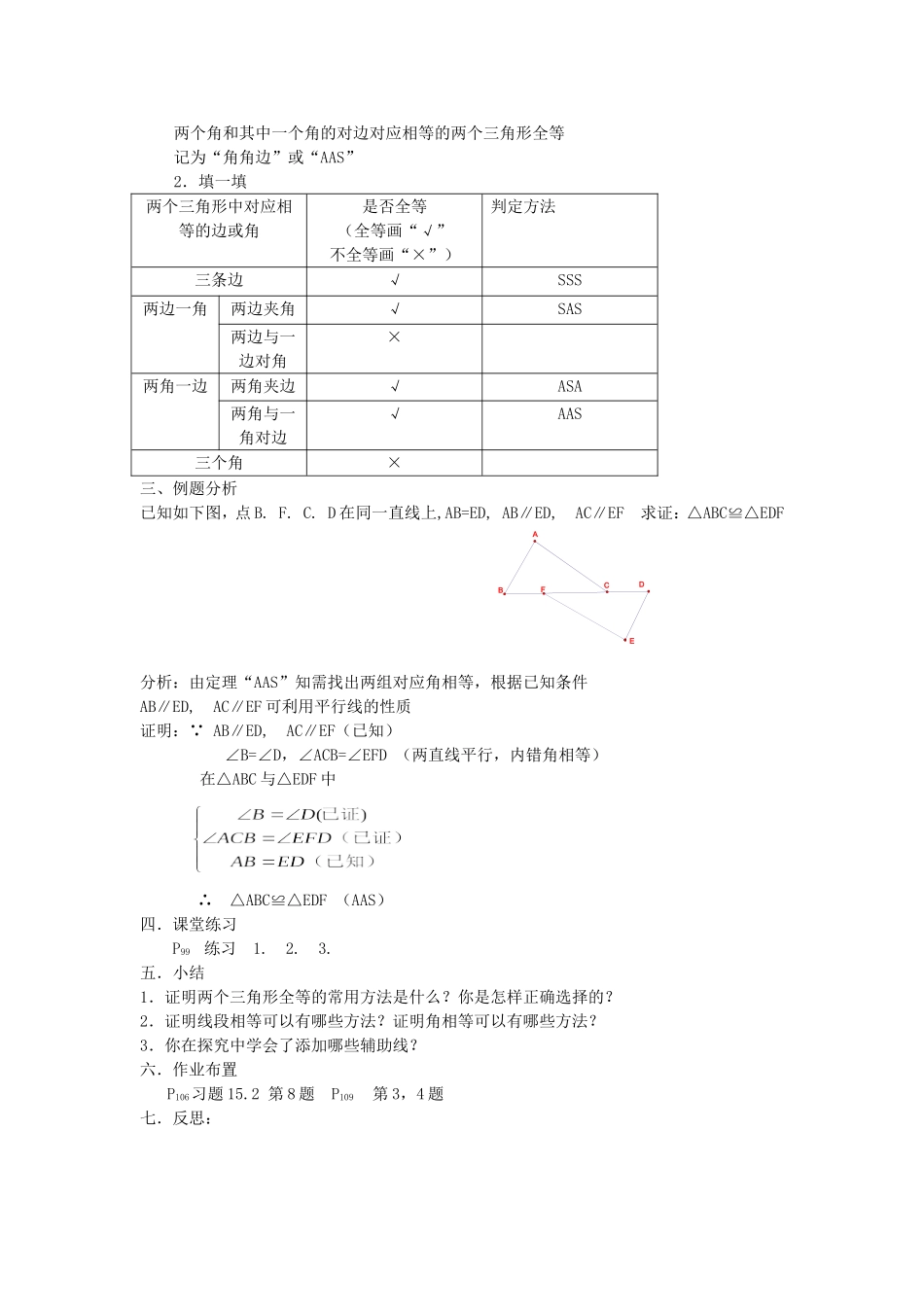
14.2三角形全等的判定(四)教学目标1.知识与技能理解用“角角边”来判定两个三角形全等的方法,发展推理意识2.过程与方法经历探索判定两个三角形全等的方法,挖掘思维潜能。3.情感态度与价值观培养合情推理意识,提升证明问题的能力教学重点应用“角角边”判定两个三角形全等教学难点怎样运用已学过的判定三角形全等的方法解决实际问题。教学过程一、创设情境,引入新课已知如下图所示,D在AB上,E在AC上,AB=AC,∠B=∠C求证:AD=AEACBED分析:找到和已知条件有关的△ACD和△ABE,利用“ASA”证明出它们全等,从而得到AD=AE证明:在△ACD与△ABE中∴△ACD≌△ABE(ASA)∴AD=AE(全等三角形的对应边相等)变式问题:如果将上题中的已知条件∠B=∠C,改写成∠AEB=∠ADC,你能证出AD=AE吗?试一试!分析:在△ACD中,∠C=180°-∠A-∠ADC,同样∠B=180°-∠A-∠AEB.所以有∠A=∠A,∠ADC=∠AEB可转化出∠B=∠C.再利用“ASA”来证明△ACD≌△ABE.从而有AD=AE.我们发现:两个角和其中一个角的对边对应相等的两个三角形全等。即“AAS”我们可这样证明证明:在△ACD与△ABE中∴△ACD≌△ABE(AAS)∴AD=AE二、新课讲解1.全等三角形判定定理4:两个角和其中一个角的对边对应相等的两个三角形全等记为“角角边”或“AAS”2.填一填两个三角形中对应相等的边或角是否全等(全等画“√”不全等画“×”)判定方法三条边√SSS两边一角两边夹角√SAS两边与一边对角×两角一边两角夹边√ASA两角与一角对边√AAS三个角×三、例题分析已知如下图,点B.F.C.D在同一直线上,AB=ED,AB∥ED,AC∥EF求证:△ABC≌△EDFABDCFE分析:由定理“AAS”知需找出两组对应角相等,根据已知条件AB∥ED,AC∥EF可利用平行线的性质证明:∵AB∥ED,AC∥EF(已知)∠B=∠D,∠ACB=∠EFD(两直线平行,内错角相等)在△ABC与△EDF中∴△ABC≌△EDF(AAS)四.课堂练习P99练习1.2.3.五.小结1.证明两个三角形全等的常用方法是什么?你是怎样正确选择的?2.证明线段相等可以有哪些方法?证明角相等可以有哪些方法?3.你在探究中学会了添加哪些辅助线?六.作业布置P106习题15.2第8题P109第3,4题七.反思: