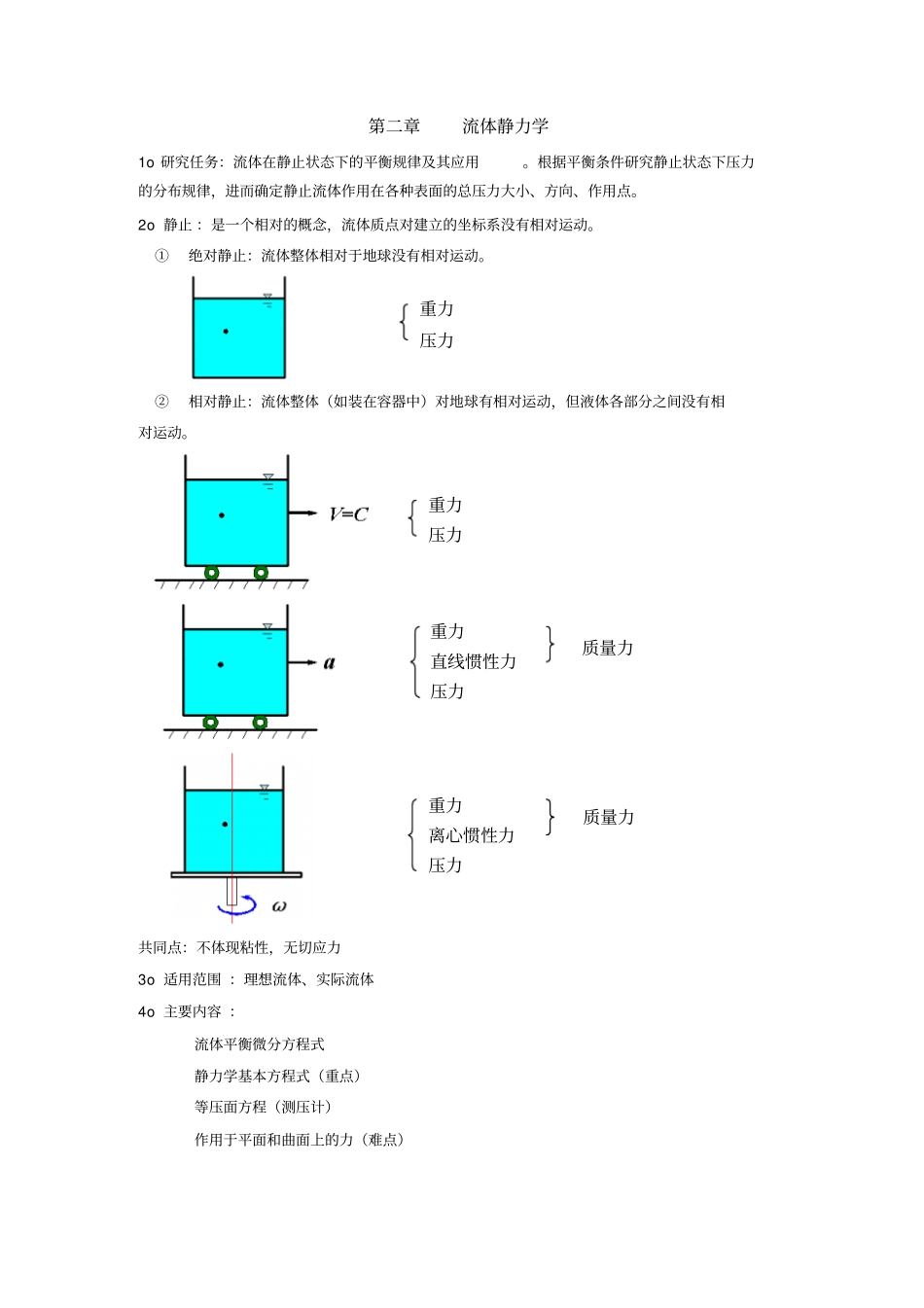
第二章流体静力学1o研究任务:流体在静止状态下的平衡规律及其应用。根据平衡条件研究静止状态下压力的分布规律,进而确定静止流体作用在各种表面的总压力大小、方向、作用点。2o静止:是一个相对的概念,流体质点对建立的坐标系没有相对运动。①绝对静止:流体整体相对于地球没有相对运动。②相对静止:流体整体(如装在容器中)对地球有相对运动,但液体各部分之间没有相对运动。共同点:不体现粘性,无切应力3o适用范围:理想流体、实际流体4o主要内容:流体平衡微分方程式静力学基本方程式(重点)等压面方程(测压计)作用于平面和曲面上的力(难点)重力压力重力压力重力直线惯性力压力重力离心惯性力压力质量力质量力第一节流体静压强及其特性一、基本概念1、流体静压强:静止流体作用在单位面积上的力。p设微小面积A上的总压力为P,则平均静压强:APp点静压强:APpAlim0即流体单位面积上所受的垂直于该表面上的力。单位:N/m2(Pa)2、总压力:作用于某一面上的总的静压力。P单位:N(牛)3、流体静压强单位:国际单位:N/m2=Pa物理单位:dyn/cm21N=105dyn,1Pa=10dyn/cm2工程单位:kgf/m2混合单位:1kgf/cm2=1at(工程大气压)≠1atm(标准大气压)1at=1kgf/cm2=9.8×104Pa=10m水柱1atm=1.013×105Pa=10.3m水柱二、流体静压强特性1、静压强作用方向永远沿着作用面内法线方向——方向特性。(垂直并指向作用面)证明:反证法证明之。有一静止流体微团,用任意平面将其切割为两部分,取阴影部分为隔离体。设切割面上任一点m处静压强方向不是内法线方向,则它可分解为np和切应力。而静止流体既不能承受切应力,也不能承受拉应力,如果有拉应力或切应力存在,将破坏平衡,这与静止的前提不符。所以静压强p的方向只能是沿着作用面内法线方向。2、静止流体中任何一点上各个方向的静压强大小相等,而与作用面的方位无关,即p只是位置的函数p=p(x,y,z)——大小特性。(各向相等)ΔAΔP证明思路:1、选取研究对象(微元体)2、受力分析(质量力与表面力)3、导出关系式0F4、得出结论1、选取研究对象(微元体)从静止流体中取出一微小四面体OABC,其坐标如图,三个垂直边的长度分别为dx、dy、dz,设xp、yp、zp、np(n方向是任意的)分别表示作用在OAC、OBC、OAB、ABC表面上的静压强,np与x、y、z轴的夹角为、、。2、受力分析(质量力与表面力)流体微元所受力分为两类:表面力和质量力。(1)表面力表面力与作用面的面积成正比。作用在OAC、OBC、OAB、ABC面上的总压力分别为:(特性一:垂直并指向作用面)(2)质量力质量力与微元体的体积成正比。四面体的体积:dxdydzVOABC61四面体的质量:dxdydzM61设单位质量流体的质量力在坐标轴方向上的分量为X、Y、Z,则质量力F在坐标轴方向的分量是:3、导出关系式0F因流体微团平衡,据平衡条件,其各方向作用力之和均为零。则在x方向上,有:将上面各表面力、质量力表达式代入后得又cosdA即为ABC在yoz平面上的投影面积,则当dx、dy、dz趋于零时也就是四面体缩小到o成为一个质点时,有:同理:nypp即:nzyxpppp4、得出结论因n方向是任意选定的,故上式表明,静止流体中同一点各个方向的静压强均相等。在连续介质中,p仅是位置坐标的连续函数p=p(x,y,z).说明:以上特性不仅适用于流体内部,而且也适用于流体与固体接触的表面。如:同一点受力各向相等,但位置不同,大小不同。呈什么关系?=》第二节中讨论第二节流体平衡微分方程式一、方程式的建立它是流体在平衡条件下,质量力与表面力所满足的关系式。根据流体平衡的充要条件,静止流体受的所有力在各个坐标轴方向的投影和都为零,可建立方程。方法:微元分析法。在流场中取微小六面体,其边长为dx、dy、dz,然后进行受力分析,列平衡方程。以x轴方向为例,如图所示1、取研究对象微元体:无穷小平行六面体,dx、dy、dz→0微元体中心:A(x,y,z)A1点坐标:A1(x-dx/2,y,z)A2点坐标:A2(x+dx/2,y,z)2、受力分析(1)表面力设A处压强:p(x,y,z)因压强分布是坐标的连续函数,则A1点、A2点的压强p1、p2可按泰勒级数展开,略去二阶以上无穷小量,得到A1、A2处的压强分别为:则表面力在x方向的合...