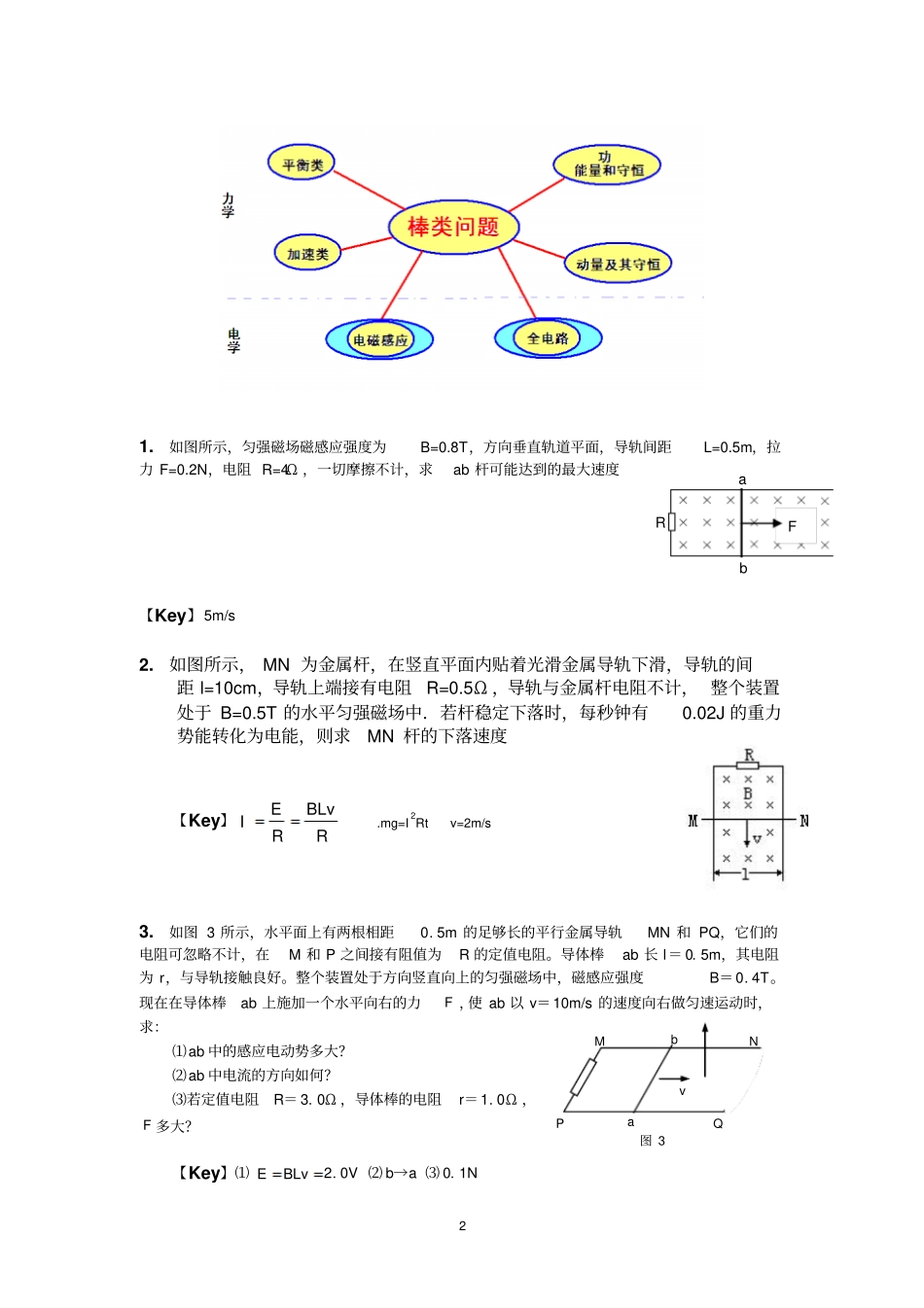
1R1R2vAaBb高二物理第★-03-★次培优材料电磁感应单棒问题双棒问题1.两个闭合铝环,挂在一根水平光滑的绝缘杆上,当条形磁铁N极向左插向圆环时(如图),两圆环的运动是A.边向左移边分开B.边向左移边靠拢C.边向右移边分开D.边向右移边靠拢2.如图所示,导线ab沿金属导轨运动,使电容器c充电,设磁场是匀强磁场,且右边回路电阻不变,若使电容器带电量恒定,且上板带正电,则ab的运动情况是()A.匀速向右运动B.匀加速向左运动C.变加速向左运动D.匀加速向右运动3.图中的匀强磁场磁感应强度B=0.5T,让长为0.2m的导体AB在金属导轨上,以5m/s的速度向左做匀速运动,设导轨两侧所接电阻R1=4Ω,R2=1Ω,本身电阻为1Ω,AB与导轨接触良好。求:(1)导体AB中的电流大小(2)全电路中消耗的电功率【Key】(1)0.28A(2)0.14w楞次定律你掌握了吗?单棒问题2abRF1.如图所示,匀强磁场磁感应强度为B=0.8T,方向垂直轨道平面,导轨间距L=0.5m,拉力F=0.2N,电阻R=4Ω,一切摩擦不计,求ab杆可能达到的最大速度【Key】5m/s2.如图所示,MN为金属杆,在竖直平面内贴着光滑金属导轨下滑,导轨的间距l=10cm,导轨上端接有电阻R=0.5Ω,导轨与金属杆电阻不计,整个装置处于B=0.5T的水平匀强磁场中.若杆稳定下落时,每秒钟有0.02J的重力势能转化为电能,则求MN杆的下落速度【Key】RBLvREI.mg=I2Rtv=2m/s3.如图3所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R的定值电阻。导体棒ab长l=0.5m,其电阻为r,与导轨接触良好。整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T。现在在导体棒ab上施加一个水平向右的力F,使ab以v=10m/s的速度向右做匀速运动时,求:⑴ab中的感应电动势多大?⑵ab中电流的方向如何?⑶若定值电阻R=3.0Ω,导体棒的电阻r=1.0Ω,F多大?【Key】⑴BLvE2.0V⑵b→a⑶0.1NMNPQabv图334.如图所示,电阻不计的平行金属导轨MN和OP水平放置,MO间接有阻值为R的电阻,导轨相距为d,其间有竖直向下的匀强磁场,磁感强度为B.质量为m、电阻为r的导体棒CD垂直于导轨放置,并接触良好.用平行于MN的恒力F向右拉动CD,CD受恒定的摩擦阻力.f,已知F>f.问:(1)CD运动的最大速度是多少?(2)当CD达到最大速度后,电阻R消耗的电功率是多少?(3)当CD的速度是最大速度的1/3时,CD的加速度是多少?解析:(1)以金属棒为研究对象,当CD受力:F=FA+f时,CD速度最大,即:2222))((dBrRfFvfrRvdBfBIdFmm(2)CD棒产生的感应电动势为:BdrRfFBdvEm))((回路中产生的感应电流为:BdfFrREI则R中消耗的电功率为:2222)(dBRfFRIRP(3)当CD速度为最大速度的1/3即mvv31时,CD中的电流为最大值的1/3即II31'则CD棒所受的安培力为:)(31''fFdBIFACD棒的加速度为:mfFmFfFaA3)(2'5.如图5所示,有两根足够长、不计电阻,相距L的平行光滑金属导轨cd、ef与水平面成θ角固定放置,底端接一阻值为R的电阻,在轨道平面内有磁感应强度为B的匀强磁场,方向垂直轨道平面斜向上.现有一平行于ce、垂直于导轨、质量为m、电阻不计的金属杆ab,在沿轨道平面向上的恒定拉力F作用下,从底端ce由静止沿导轨向上运动,当ab杆速度达到稳定后,撤去拉力F,最后ab杆又沿轨道匀速回到ce端。已知ab杆向上和向下运动的最大速度相等。求:(1)拉力F大小;(2)杆ab最后回到ce端的速度vθaFbRcdefB图54【Key】(1)sin2mgF(2)22sinLBmgRv6.如图6所示,宽度为L的足够长的平行金属导轨MN、PQ的电阻不计,垂直导轨水平放置一质量为m电阻为R的金属杆CD,整个装置处于垂直于导轨平面的匀强磁场中,导轨平面与水平面之间的夹角为θ,金属杆由静止开始下滑,动摩擦因数为μ,下滑过程中重力的最大功率为P,求磁感应强度的大小。【Key】B=mgLRsinθ(sinθ-μcosθ)P7.如图所示,足够长的金属导轨MN和PQ与R相连,平行地放在水平桌面上,质量为m的金属杆可以无摩擦地沿导轨运动.导轨与ab杆的电阻不计,导轨宽度为L,磁感应强度为B的匀强磁场垂直穿过整个导轨平面.现给金属杆ab一个瞬时冲量I0,使ab杆向右滑行.(1)求回路的最大电流.(2)当滑行过程中电阻上产生的热量为Q时,杆ab的加速度多大...