锐角三角函数--余弦、正切(黄美萍)VIP免费

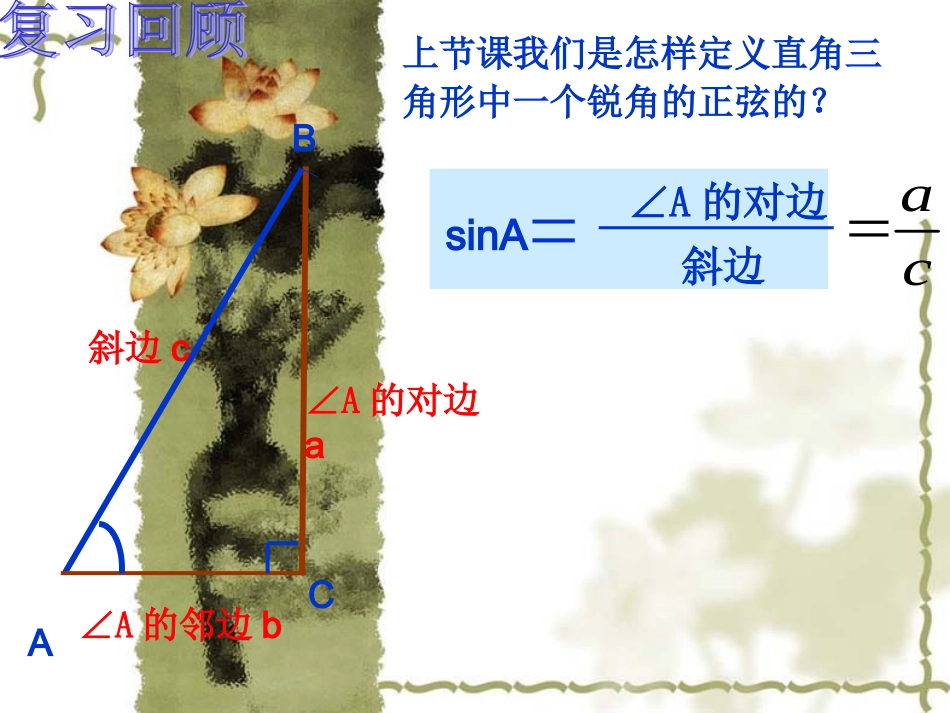
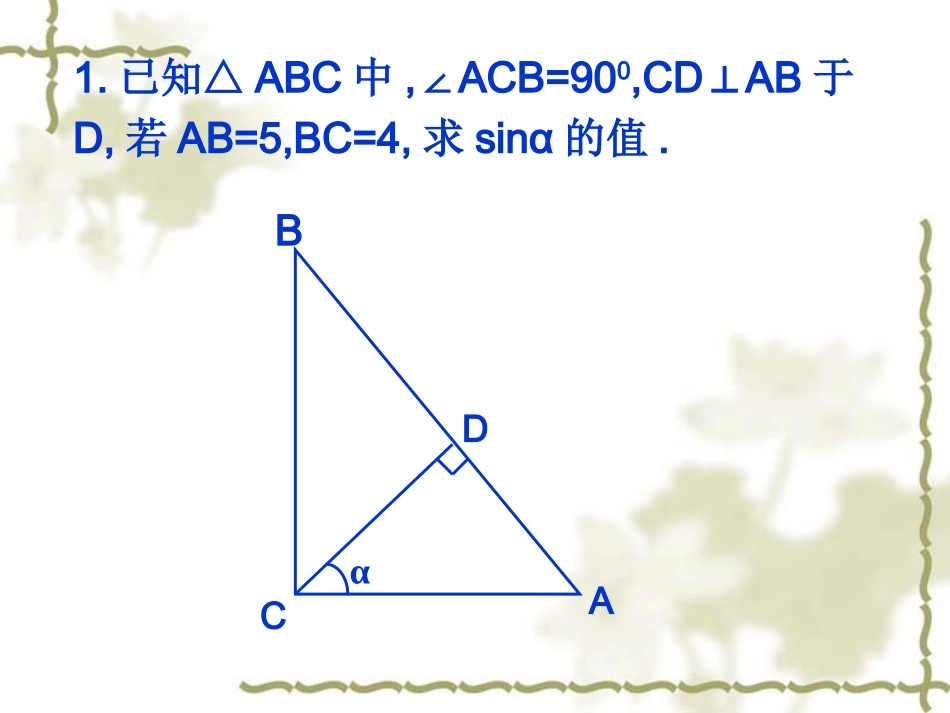
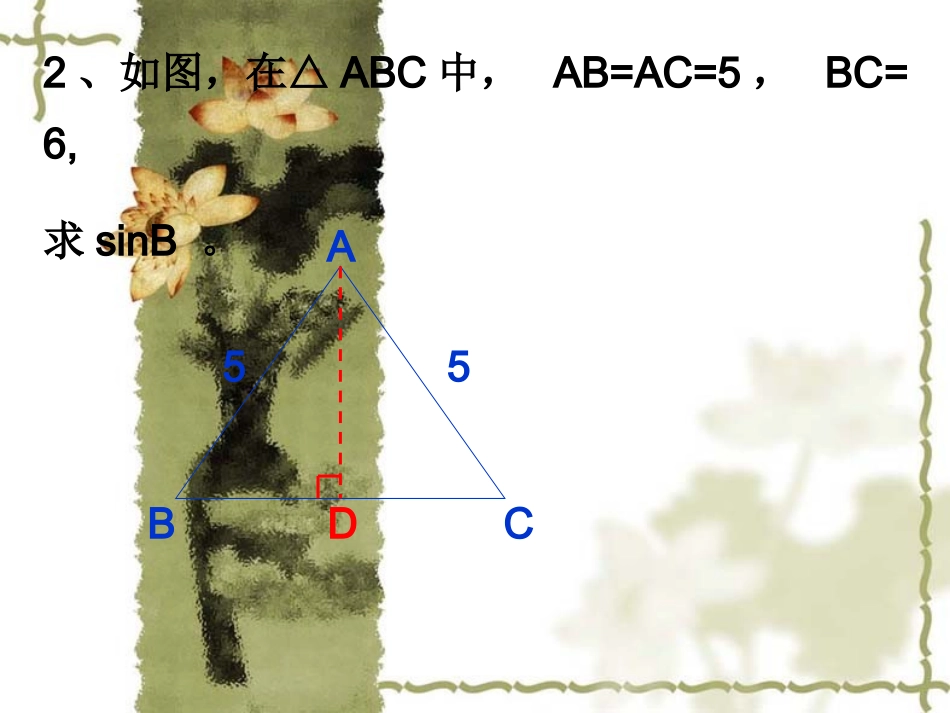
∠A的对边sinA斜边∠A的对边aABC∠A的邻边b斜边c上节课我们是怎样定义直角三角形中一个锐角的正弦的？ca1.已知△ABC中,ACB=90∠0,CDAB⊥于D,若AB=5,BC=4,求sinα的值.BACDα2、如图，在△ABC中，AB=AC=5，BC=6,求sinB。DABC553.角的正弦值的计算:(1)直接在直角三角形中利用定义计算。(2)通过构造直角三角形进行计算。(3)转化为求与之相等的角的正弦值。28.1锐角三角函数(2)——余弦、正切【问题】如图，在Rt△ABC中，∠C＝90°，当锐角A确定时，∠A的对边与斜边的比就随之确定，此时，其他边之间的比是否也确定了呢？为什么？ABC邻边b对边a斜边c【探究】观察图中的Rt△ABC和RtA△/B/C/中，它们之间有什么关系？此时又分别等于哪两条线段的比？ACBCABAC,AB/C/BC┏一般地,在RtABC△中，∠C=90°,把∠A的对边与邻边的比叫做∠A的正切正切（tangent），记作tantanAA，即baAAA的邻边的对边tan锐角A的正弦、余弦、正切都叫做∠A的锐角三角函数．一般地,在RtABC△中，∠C=90°,我们把∠A的邻边与斜边的比叫做∠A的余弦余弦（cosine），记作coscosAA，即cbAA斜边的邻边cosABC邻边b对边a斜边c∠B的正切如何表示呢?【试一试】1、在Rt△ABC中，∠C=90°，∠A=30°，求sinA,cosA,tanA的值。ABC若∠A=45°，求sinA,cosA,tanA的值。2、在Rt△ABC中，∠C=90°，AB=13，AC=12，求sinA,cosA,tanA的值。ABC例1：如图，在RtABC△中，∠C=90°，求cosA、tanA、cosB和tanB的值(1)CBA43(2)CBA513例题示范例1如图，在Rt△ABC中，∠C＝90°，BC＝6，sinA＝，求cosA、tanB的值．53ABC6例题示范例３、在△ABC中，AB=AC＝4，BC=6，求∠B的三角函数值。例４、已知∠A为锐角，sinA＝，求cosA、tanA的值。17151.分别求出下列直角三角形中两个锐角的正弦值、余弦值和正切值．练习ABC13122.在Rt△ABC中，如果各边长都扩大2倍，那么锐角A的正弦值、余弦值和正切值有什么变化？3.如图，在Rt△ABC中，∠C＝90°，AC＝8，tanA＝，求：sinA、cosB的值．43如图，在Rt△ABC中，∠ACB＝90°，CD是AB边上的高。求：sinA==;cosA==;tan∠ACD==．练一练CDBA例2已知锐角α的始边在x轴的正半轴上，顶点在原点，终边上有一点P的坐标为（2，3），求∠α的三个三角函数值.例题示范xyOP(2,3).┓A如图，在矩形ABCD中，AB=10，BC=8，E为AD上的一点，沿CE将△CDE对折，点D正好落在AB边的F上。求tanAFE∠的值。【探索提高】ABCDEF直线m与y轴交点的纵坐标为-3，与x轴相交所成的锐角为α，若tanα=3/4，求直线m的解析式。【探索提高】=ac斜边的对边AsinA=课堂小结1、锐角三角函数的概念。=bc斜边的邻边AcosA==ab的邻边的对边AAtanA=2、利用定义进行计算。sinA、cosA、tanA的大小只与∠A的大小有关，而与直角三角形的边长无关。3、直角三角形两个锐角的三角函数之间的关系：如上图：sinA=cosBcosA=sinBtanA.tanB=1今天作业：1作业本（1）P19作业本（2）P182课时作业本P76---77