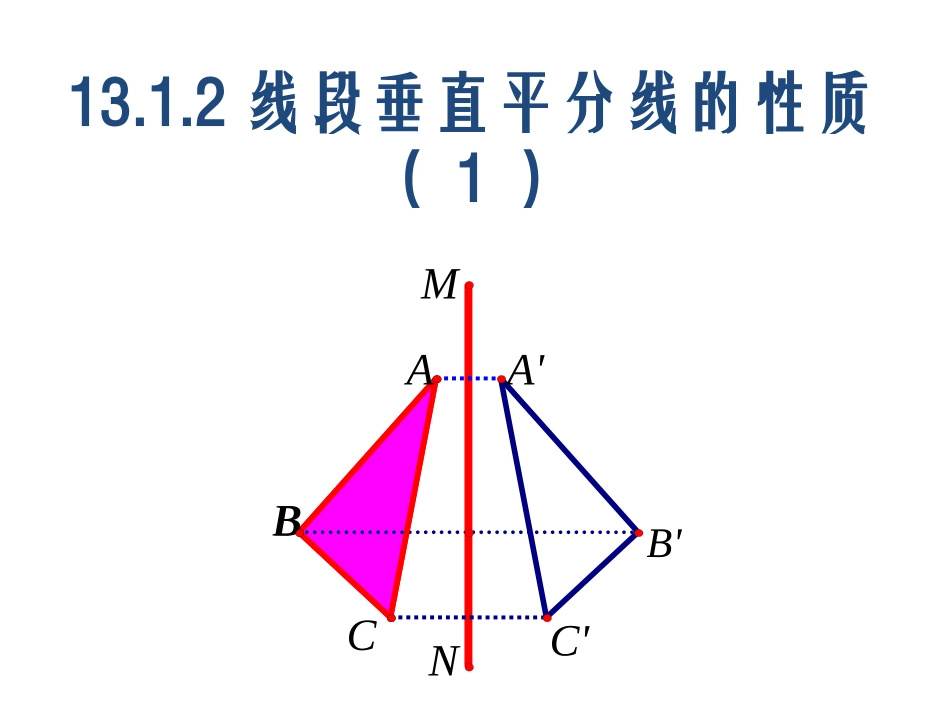
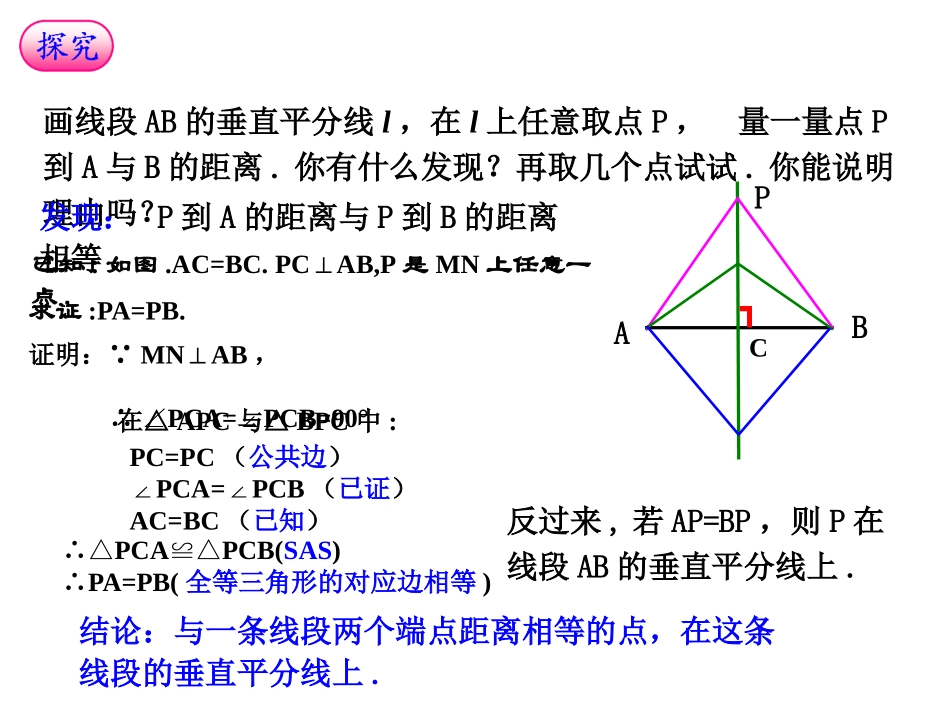
13.1.2线段垂直平分线的性质(1)C'A'CABBMNB'1.如果沿一条直线折叠,直线两旁的部分能够,这个图形就叫做轴对称图形,这条直线就是它的。2.把沿着某一条直线折叠,如果它能够与另一个图形,那么就说这两个图形关于这条直线(成轴)对称,这条直线叫做,折叠后重合的点是对应点,叫做。3.经过线段并且于这条线段的直线,叫做线段的垂直平分线。4.对称轴与对应点连线的关系:对称轴是任何一对对应点所连线段的。课前检测:画线段AB的垂直平分线l,在l上任意取点P,量一量点P到A与B的距离.你有什么发现?再取几个点试试.你能说明理由吗?PAB┓发现:P到A的距离与P到B的距离相等.C已知:如图.AC=BC.PCAB,P⊥是MN上任意一点.求证:PA=PB.∴△PCAPCB(≌△SAS)∴PA=PB(全等三角形的对应边相等)证明:∵MNAB⊥,∴∠PCA=PCB=90°∠在△APC与△BPC中:PC=PC(公共边)∠PCA=PCB∠(已证)AC=BC(已知)反过来,若AP=BP,则P在线段AB的垂直平分线上.结论:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.AB已知:两点A、B,和点A、B的距离相等的点应在什么位置?性质定理:在线段垂直平分线上的点到线段两个端点距离都相等.逆定理:与线段两个端点距离相等的点都在线段的垂直平分线上.线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合.常用于证明线段相等角的平分线ODEABPC定理1在角的平分线上的点到这个角的两边的距离相等。定理2到一个角的两边的距离相等的点,在这个角的平分线上。角的平分线是到角的两边距离相等的所有点的集合线段的垂直平分线定理线段垂直平分线上的点和这条线段两个端点的距离相等。逆定理和一条线段两个端点距离相等的点,在这条线段的垂直平分线上。线段的垂直平分线可以看作是和线段两个端点距离相等的所有点的集合ABMNP点的集合是一条射线点的集合是一条直线[活动3]牛刀小试EOPDCBA1、已知:如图,PD⊥OA于D,PE⊥OB于E,PD=PE,可得结论:。2、如图PA=PB,可得结论:。当堂检测:[活动4]ABDCE1、如图直线L为△ABC的边BC的垂直平分线,交AB于E,连接EC,AB=5,AC=4,则△AEC的周长为:。2、在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,求△ABC的周长。3.在△ABC中,∠ACB=90°,AB=8cm,BC的垂直平分线DE交AB于D点,则CD=_____.EDCBA4cm4、在△ABC,PM,QN分别垂直平分AB,AC,则:(1)若BC=10cm则△APQ的周长=_____cm;(2)若∠BAC=100°则∠PAQ=______.QNMCBPA1020°[活动5]归纳总结1、线段垂直平分线的定义:。2、线段垂直平分线的性质:。3、线段垂直平分线的判定:。课后巩固:ADECBFG1、如图BC比AC长2cm,AB的垂直平分线交BC于D,交AB于E,△ACD的周长是14cm,求BC和AC的长。2、如图AD是,∠BAC的平分线,DE⊥AB,DF⊥AC,垂足分别为E,F,连接EF,EF与AD交于点G。求证:AD垂直平分EF。