1.5--三角函数的应用VIP免费

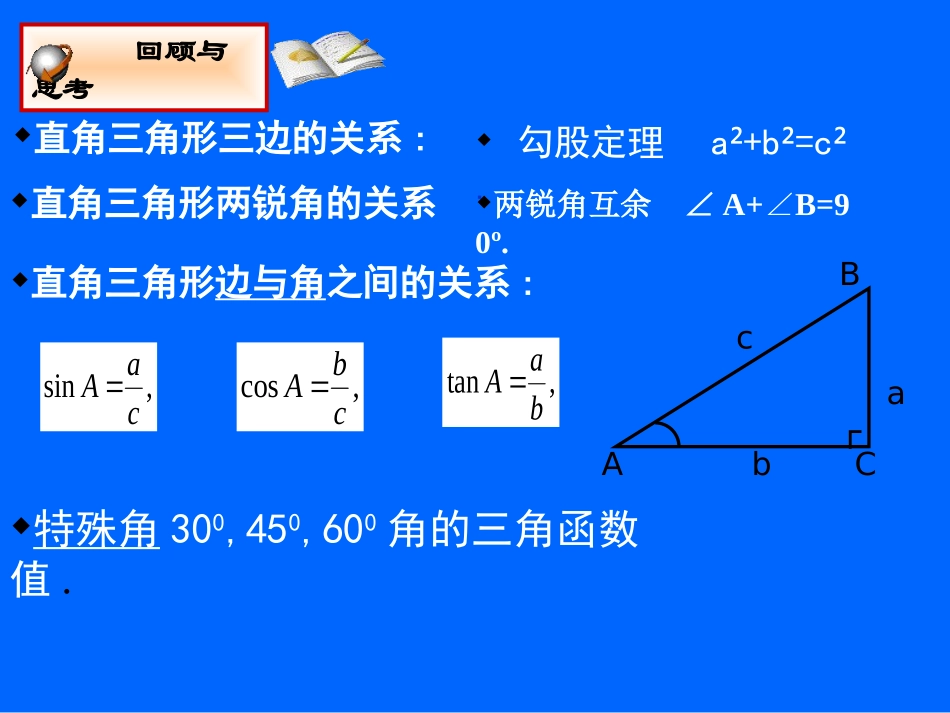
北师大版九年级数学(下)第一章1.5三角函数的应用建平县第二中学执教者：邵国良直角三角形两锐角的关系直角三角形三边的关系:回顾与思考bABCa┌c特殊角300,450,600角的三角函数值.直角三角形边与角之间的关系:,sincaA,coscbA,tanbaA勾股定理a²+b²=c².两锐角互余∠A+∠B=90º.31试一试1、如图,根据图中已知数据,求△ABC的BC边上的高和△ABC的面积.（近似取1.7）温馨提示：考虑用方程解：设AD的长为Xcm∵在RtA△DC,∠ACD=45º∵在RtABC△中，∠B=30º,∴CD=AD=X∴△ABC的面积=X4X∴tan30º=ADBD=4xx1.7x=x+4x=340即边上的高是cm34021340=3803ABC4503004cmD┌2、如图,根据图中已知数据,求AD.做一做ABC55025020D┌老师的提示:你认为本题的解法与上题有什么区别和联系。由1、2两题的做法、你得到了哪些经验(sin25º≈0.4tan25º≈0.5sin55º≈0.8tan55º≈1.4)这两题属于一种类型，它们可用类似的方法解决，要用列方程的方法来解决。古塔究竟有多高如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).想一想要解决这个问题,我们仍需将其数学化.请与同伴交流你是怎么想的?准备怎么去做?现在你能完成这个任务吗?xACxBCDABC┌50m300600.30tan,60tan00xBCxAC.5030tan60tan00xx.433253335030tan60tan5000mx答:该塔约有43m高.解法1:如图,根据题意知,∠A=300,∠DBC=600,AB=50m.老师期望:这道题你能有更简单的解法.设CD=x,则∠ADC=60º,BDC=30∠º,在RtA△DC中,tan60º=在Rt△BDC中,tan30º=∵AC-BC=AB50DC3例题欣赏解法2:如图,根据题意知,A=30∠º,DBC=60∠º,AB=50m.则∠ADC=60º,BDC=30∠º,DABC┌50m300600∴∠BDA=30º∴∠A=B∠DA∴BD=AB=50在Rt△DBC中,DBC=60∠ºsin60º=∴DC=50×sin60º=2543(m)答:该塔约有43m高老师提示：本题的解法你又得到了哪些经验？楼梯加长了多少某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).做一做现在你能完成这个任务吗?请与同伴交流你是怎么想的?准备怎么去做?ABCD┌练习展示解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(1)AB-BD的长,(2)AD的长.ABCD┌4m350400,40sin0BDBC.40sin0BDBC,35sin0ABBC答:调整后的楼梯会加长约0.48m..48.45736.06428.0435sin45sin35sin000mBDBCAB.48.0448.4mBDAB练习展示解:如图,根据题意可知,∠A=350,∠BDC=400,DB=4m.求(2)AD的长.,40tan0DCBC.40tan0BCDC,35tan0ACBC答:楼梯多占约0.61m一段地面..35tan0BCACDCACAD0040tan135tan1BC00040tan135tan140sinBD.61.0mABCD┌4m350400钢缆长多少如图,一灯柱AB被一钢缆CD固定.CD与地面成400夹角,且DB=5m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?(结果精确到0.01m).随堂练习怎么做?我先将它数学化!EBCD2m4005m解:如图,根据题意可知,∠CDB=400,EC=2m,DB=5m.求DE的长.练习解答∴∠BDE≈51.12°.,40tan0BDBC,12.51cos0DEDB答:钢缆ED的长度约为7.97m..40tan0BDBC).(1955.6240tan20mBDBCBE.24.15240tan5tan0BDBEBDE.97.76277.0512.51cos0mDBDEEBCD2m4005m•由锐角的三角函数值求锐角小结拓展填表:已知一个角的三角函数值,求这个角的度数(逆向思维)∠A=30º∠A=60º∠A=45º∠A=60º∠A=30º∠A=45º∠A=30º∠A=60º∠A=45º21sinA21cosA33tanA23sinA22cosA3tanA23cosA1tanA知识的升华独立作业P24习题1.61,2,3题;祝你成功！结束寄语希望你通过今天的努力学习将来为国家和社会做出更大的贡献！下课了!