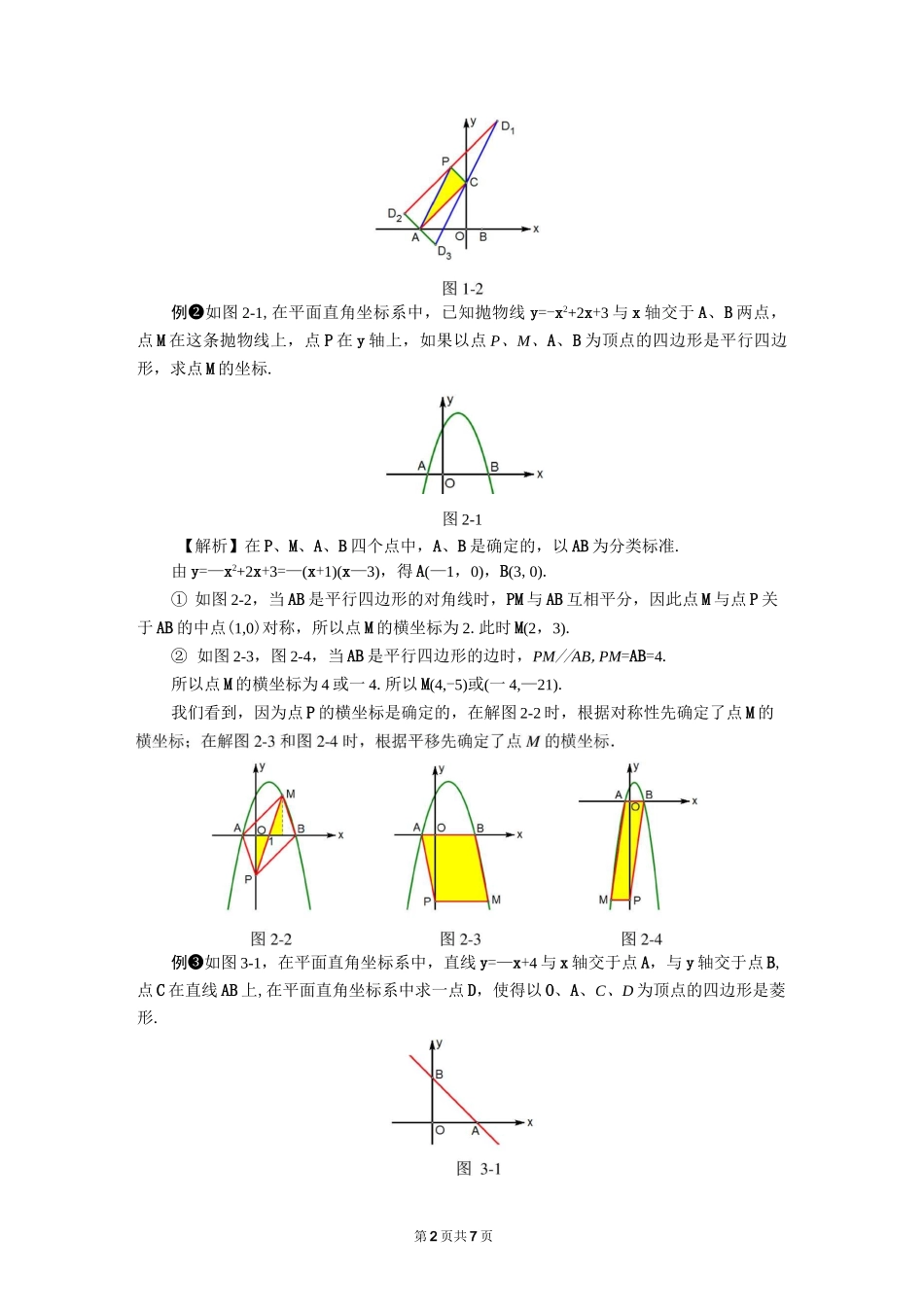
第1页共7页中考数学压轴题解题策略平行四边形的存在性问题解题策略专题攻略解平行四边形的存在性问题一般分三步:第一步寻找分类标准,第二步画图,第三步计算.难点在于寻找分类标准,分类标准寻找的恰当,可以使解的个数不重复不遗漏,也可以使计算又好又快.如果已知三个定点,探寻平行四边形的第四个顶点,符合条件的有3个点:以已知三个定点为三角形的顶点,过每个点画对边的平行线,三条直线两两相交,产生3个交点.如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况.根据平行四边形的对边平行且相等,灵活运用坐标平移,可以使得计算过程简便.根据平行四边形的中心对称的性质,灵活运用坐标对称,可以使得解题简便.例题解析例❶如图1-1,在平面直角坐标系中,已知抛物线P样y=—x2—2x+3与x轴交于A、B两点(A在B的左侧),与y轴交于点C,顶点为P,如果以点P、A、C、D为顶点的四边形是平行四边形,求点D的坐标.【解析】P、A、C三点是确定的,过\FAC的三个顶点分别画对边的平行线,三条直线两两相交,产生3个符合条件的点D(如图1-2).由y=—x2—2x+3=—(x+1)2+4,得A(—3,0),C(0,3),P(—1,4).由于A(—3,0)右3,上3C(0,3),所以P(—1,4)右3,上3卩(2,7).1由于C(0,3)下3,左34(—3,0),所以P(—1,4)下3,左3D2(—4,1).2由于P(—1,4)右1,下1,C(0,3),所以A(—3,0)右1,下1,D3(—2,—1).我们看到,用坐标平移的方法,远比用解析式构造方程组求交点方便多了.图1-第2页共7页例❷如图2-1,在平面直角坐标系中,已知抛物线y=-x2+2x+3与x轴交于A、B两点,点M在这条抛物线上,点P在y轴上,如果以点P、M、A、B为顶点的四边形是平行四边形,求点M的坐标.图2-1【解析】在P、M、A、B四个点中,A、B是确定的,以AB为分类标准.由y=—x2+2x+3=—(x+1)(x—3),得A(—1,0),B(3,0).①如图2-2,当AB是平行四边形的对角线时,PM与AB互相平分,因此点M与点P关于AB的中点(1,0)对称,所以点M的横坐标为2.此时M(2,3).②如图2-3,图2-4,当AB是平行四边形的边时,PM//AB,PM=AB=4.所以点M的横坐标为4或一4.所以M(4,-5)或(一4,—21).我们看到,因为点P的横坐标是确定的,在解图2-2时,根据对称性先确定了点M的例❸如图3-1,在平面直角坐标系中,直线y=—x+4与x轴交于点A,与y轴交于点B,点C在直线AB上,在平面直角坐标系中求一点D,使得以O、A、C、D为顶点的四边形是菱形.第3页共7页【解析】由y=-x+4,得A(4,0),直线AB与坐标轴的夹角为45°.在O、A、C、D四个点中,O、A是确定的,以线段OA为分类标准.如图3-2,如果OA是菱形的对角线,那么点C在OA的垂直平分线上,点C(2,2)关于OA的对称点D的坐标为(2,—2).如果OA是菱形的边,那么又存在两种情况:如图3-3,以O为圆心,OA为半径的圆与直线AB的交点恰好为点B(0,4),那么正方形AOCD的顶点D的坐标为(4,4).如图3-4,以A为圆心,AO为半径的圆与直线AB有两个交点C(4-2迈,2迈)和C(4+2迈,-2迈),点C和C向左平移4个单位得到点D(-2巨,2迈)和D(2迈,-2迈).416例❹如图4-1,已知抛物线y二-x2+丁x与x轴的负半轴交于点C,点E的坐标为(0,—3),点N在抛物线的对称轴上,点M在抛物线上,是否存在这样的点M、N,使得以M、N、C、E为顶点的四边形是平行四边形?若存在,请求出点M的坐标;若不存在,请说明理由.图4-1【解析】C(—4,0)、E(0,—3)两点是确定的,点N的横坐标一2也是确定的.以CE为分类标准,分两种情况讨论平行四边形:①如图4-2,当CE为平行四边形的边时,由于C、E两点间的水平距离为4,所以M、N两点间的水平距离也为4,因此点M的横坐标为一6或2.将x=—6和x=2分别代入抛物线的解析式,得M(—6,16)或(2,16).16②如图4-3,当CE为平行四边形的对角线时,M为抛物线的顶点,所以M(-2,-―).图3-2图3-3图3-4第4页共7页整理,得7a2=1.所以a=例❺如图1,在平面直角坐标系中,抛物线y=ax2-2ax-3a(aVO)与x轴交于A、B两点(点A在点B的左侧),点D是第四象限内抛物线上的一点,直线AD与y轴负半轴交于点C,且CD=4AC.设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,求出点P的坐标;若不能,请说明理由.【解析】由y=ax2—2ax—3a=a(x+1)(x—3)...