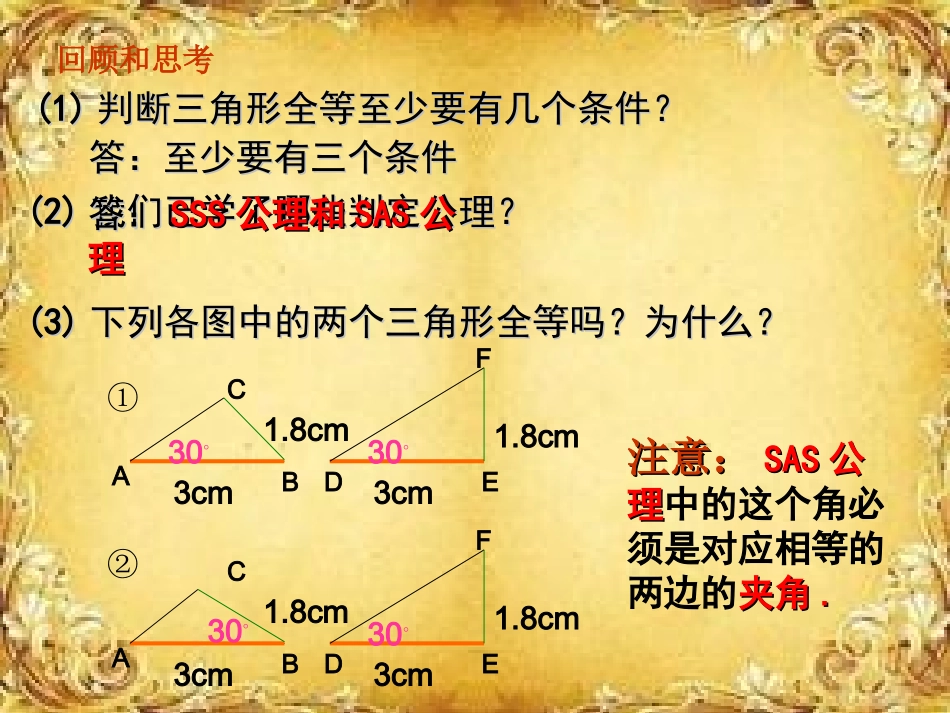
1.5.3全等三角形的判定(1)(1)判断三角形全等至少要有几个条件?判断三角形全等至少要有几个条件?答:至少要有三个条件答:至少要有三个条件(2)(2)我们已学了哪些判定公理?我们已学了哪些判定公理?答:答:SSSSSS公理和公理和SASSAS公公理理(3)(3)下列各图中的两个三角形全等吗?为什么?下列各图中的两个三角形全等吗?为什么?3cm3cm30◦30◦ADBECF1.8cm1.8cm①3cm3cm30◦30◦ADBECF1.8cm1.8cm②注意:注意:SASSAS公公理理中的这个角必须是对应相等的两边的夹角夹角..回顾和思考如图如图,,小明不慎将一块三角小明不慎将一块三角形模具打碎为两块形模具打碎为两块,,他是否他是否可以只带其中的一块碎片到可以只带其中的一块碎片到商店去商店去,,就能配一块与原来就能配一块与原来一样的三角形模具吗一样的三角形模具吗??如果如果可以可以,,带哪块去合适带哪块去合适??你能你能说明其中理由吗说明其中理由吗??问题问题和和情境情境问题问题11:如果已知一个三角形的两角及一边,那么有几:如果已知一个三角形的两角及一边,那么有几种可能的情况呢?种可能的情况呢?答:角边角(答:角边角(ASAASA)角角边()角角边(AASAAS))问题问题2:2:画△ABC,使∠∠A=60A=6000,∠,∠B=45B=4500,,AB=3cmAB=3cm。。BBAACC6060004545003cm3cm把你们所画的三角形剪下来与同桌所画的三角形进行比较,它们能互相重合吗?AABBCC6060004545003cm3cmAACC6060004545003cm3cmAACC6060004545003cm3cmAACC6060004545003cm3cmAACC6060004545003cm3cm问题问题和和探索探索有两个角和这两个角的夹边对应相等的两个有两个角和这两个角的夹边对应相等的两个三角形全等,简写成“角边角”或“三角形全等,简写成“角边角”或“ASA”ASA”三角形全等判定公理3几何语言:在△ABC与△DEF中∠B=∠E,BC=EF,∠C=F∠∴ΔABC≌DEF(ASAASA)AABBCCDDEEFF探究与探究与新知新知解: 解: ∠∠A+A+∠∠B+B+∠∠C=180°C=180°∠∠D+D+∠∠E+E+∠∠F=180°F=180°(三角形的内角和等于(三角形的内角和等于180180°°))AABBCCDDEEFF练习:如图,在练习:如图,在ΔΔABCABC和和ΔΔDEFDEF中,中,∠∠B=B=∠∠EE,,∠∠C=∠FC=∠F,,AC=DF,AC=DF,请说明请说明ΔΔABC≌ABC≌ΔΔDEFDEF∴∴∠∠A=180°-A=180°-∠∠B-B-∠∠CC∠∠D=180°-D=180°-∠∠E-E-∠∠FF ∠∠B=B=∠∠EE,∠,∠C=∠FC=∠F∴∴∠∠A=A=∠∠DD在在ΔΔABCABC和和ΔΔDEFDEF中中∠∠A=A=∠∠DDAC=DF(AC=DF(已知已知))∠∠C=∠F(C=∠F(已知已知))∴∴ΔΔABCABC≌Δ≌ΔDEFDEF((ASAASA))交流与交流与探索探索三角形全等判定公理3的推论几何语言:在△ABC与△DEF中∠B=∠E,∠C=F∠,AC=DF∴ΔABC≌DEF(AASAAS)有两个角和其中的一个角的对边对应相等的有两个角和其中的一个角的对边对应相等的两个三角形全等,简写成“角角两个三角形全等,简写成“角角边”或“边”或“AAS”AAS”AABBCCDDEEFF探究新知探究新知1.有两个角和一条边相等的两个三角形一定全等吗?AABBCCDDEEFF反例如图2.2.如图,已知∠如图,已知∠ACB=∠DFEACB=∠DFE,,BC=EFBC=EF,则应补充一个,则应补充一个直接条件直接条件----------------------------------------------------,就能使△,就能使△ABC≌△DEFABC≌△DEF。。AABBCCDDEEFF⑴∠⑴∠B=∠E(SAS)B=∠E(SAS)⑵∠⑵∠A=∠D(AAS)A=∠D(AAS)⑶⑶AC=DF(SAS)AC=DF(SAS)交流交流与与探索探索例.如图点P是∠BAC的平分线上的点,PB⊥AB,PCAC.⊥说明PB=PC的理由.ABCP角平分线的性质:角平分线上的点到叫角两边的距离距离相等. P是∠BAC的平分线上的点,且PB⊥AB,PCAC⊥∴PB=PC(角平分线上的点到叫角两边角平分线上的点到叫角两边的距离相等.的距离相等.))几何语言:探究归纳探究归纳(1)(1)完成下列推理过程:完成下列推理过程:在△在△ABCABC和△和△DCBDCB中,中,∠∠ABC=DCB∠ABC=DCB∠ BC=CBBC=CB∴△∴△ABCDCB≌△ABCDCB≌△()()ASAASAAABBCCDDOO11223344(())公共边公共边∠∠2=1∠2=1∠AASAAS∠∠33=∠=∠44∠∠22=∠=∠11CBCB==BCBC(2)(2)如如图,图,BE...