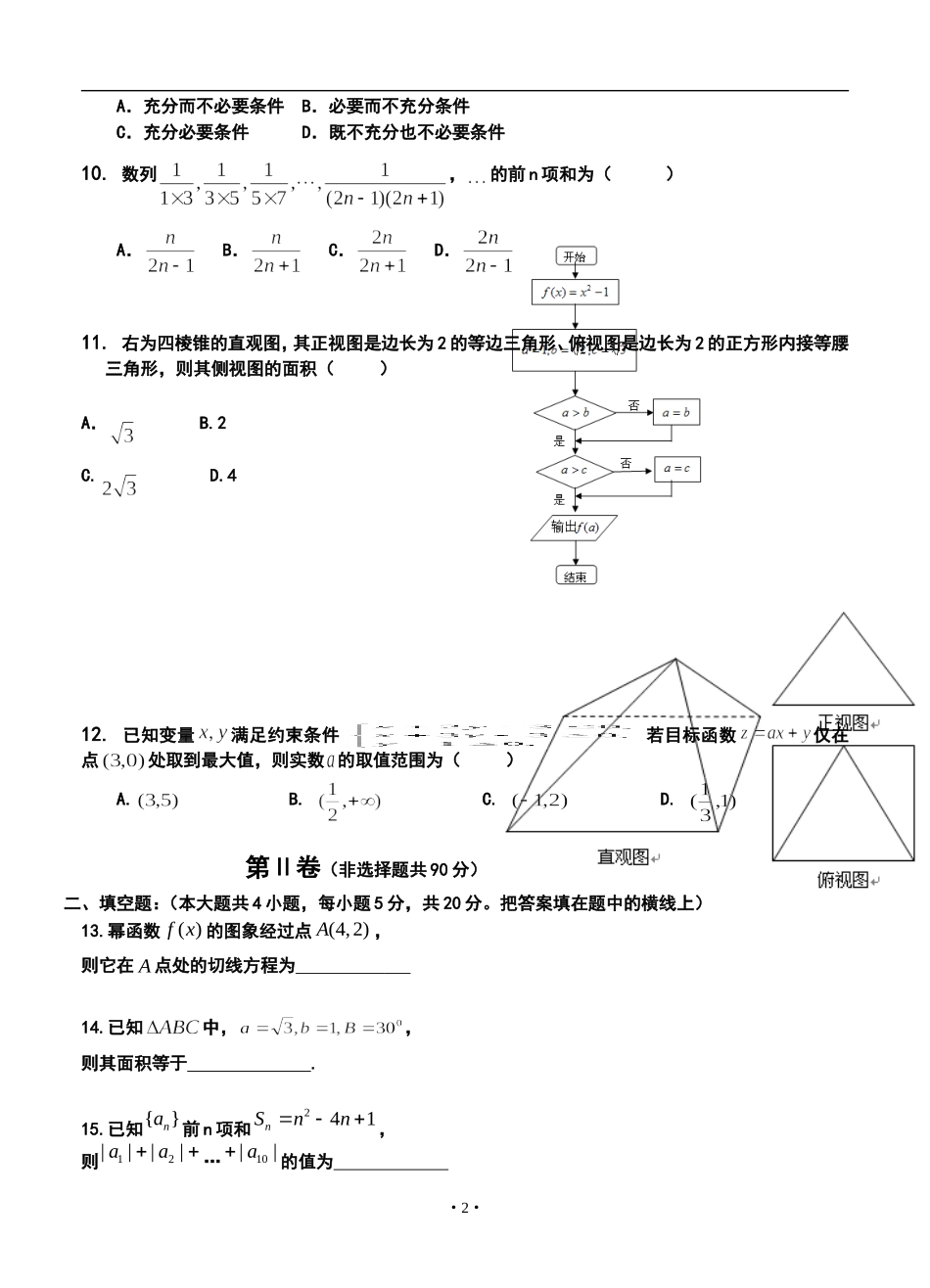
开滦二中2012届高三12月月考数学(理)试题说明:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷第1页,第Ⅱ卷第2页。第Ⅰ卷(选择题,共60分)一、选择题:(在每小题给出的四个选项中,只有一项是正确的,每小题5分,共60分.)1.若(2)aiibi,其中,abR,i是虚数单位,复数abi()A.12iB.12iC.12iD.12i2.已知集合=,={x|},且A(∁RB),则实数a的取值范围是()A.≤1B.<1C.<2D.3.函数的值域是()A.1,B.,1C.1,21D.21,04.设a、b∈R+,且,则有()A.B.C.D.5.已知等比数列的前n项和为,则x的值为()A.B.C.D.6.如果|cosθ|=,<θ<3π,那么sin的值等于()A.B.C.D.7.已知向量,,则的最大值为()A.1B.C.3D.98.在中,点P是AB上一点,且,Q是BC中点,AQ与CP交点为M,又,则的值为()A.B.C.D.9.设是等比数列,则“”是“数列是递增数列”的()·1·A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件10.数列,的前n项和为()A.B.C.D.11.右为四棱锥的直观图,其正视图是边长为2的等边三角形、俯视图是边长为2的正方形内接等腰三角形,则其侧视图的面积()A.B.2C.D.412.已知变量满足约束条件若目标函数仅在点处取到最大值,则实数的取值范围为()A.B.C.D.第Ⅱ卷(非选择题共90分)二、填空题:(本大题共4小题,每小题5分,共20分。把答案填在题中的横线上)13.幂函数)(xf的图象经过点(4,2)A,则它在A点处的切线方程为14.已知中,,则其面积等于.15.已知{}na前n项和241nSnn,则12||||aa…10||a的值为·2·1000.0250.0150.010.005908070605040·ÖÊýƵÂÊ×é¾à16.某算法流程图如图一所示,则输出的结果是三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)。17.设函数图象的一条对称轴是直线.⑴求;⑵求函数的单调增区间;⑶用五点作图法画出函数在区间上的图象.18.(本小题满分12分)某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段,…后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;(Ⅱ)估计这次考试的及格率(60分及以上为及格)和平均分;(Ⅲ)从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.19.(本小题满分12分)数列首项,前项和与之间满足(1)求证:数列是等差数列(2)求数列的通项公式20.(本小题满分12分)如图,三棱柱111ABCABC中,侧面11AACC底面ABC,112,AAACACABBC,且ABBC,O为AC中点.(Ⅰ)在1BC上确定一点E,使得//OE平面1AAB,并说明理由;(Ⅱ)求二面角11AABC的大小.·3·21.(本小题满分12分)已知:函数(其中常数).(Ⅰ)求函数的定义域及单调区间;(Ⅱ)若存在实数,使得不等式成立,求a的取值范围.22.(本小题满分10分)请考生从第A.B题中任选一题作答,如果多做,则按所做的第一题记分。A:选修4—4:坐标系与参数方程已知直线的参数方程为(t为参数),曲线C的极坐标方程为(1)求曲线C的直角坐标方程;(2)求直线被曲线C截得的弦长.B:(选修4—5:不等式选讲)(1)设a,b是非负实数,求证:22().ababab(2)求函数的最大值。·4·1ABCA1B1CO2011~2012学年第一学期高三年级月考数学试卷理答案17.解: 是函数的图像的对称轴,∴,∴.. ,∴.---------------4分⑵由⑴知,由题意得,∴函数的单调增区间.---------------8分⑶由---------------10分---------------12分18.解:(Ⅰ)因为各组的频率和等于1,故第四组的频率:-----2分直方图如右所示----------------4分(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,频率和为·5·所以,抽样学生成绩的合格率是%---------------6分利用组中值估算抽样学生的平均分==71估计这次考试的平均分是71分----------------8分(Ⅲ),,”的人数是18,15,3。所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。----------------12分20解...