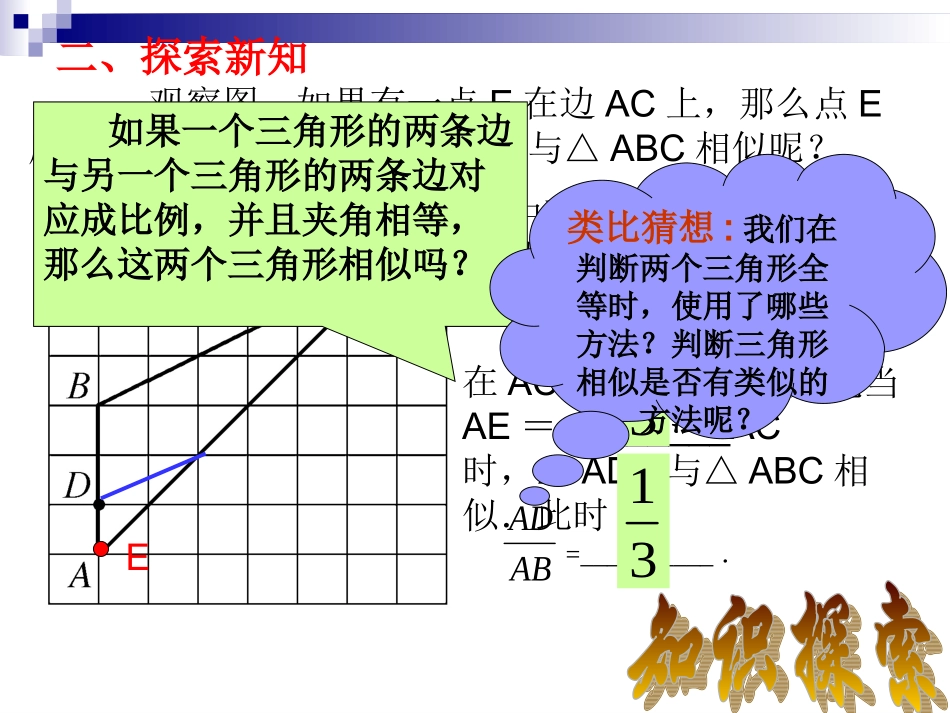
问题1:相似三角形的有关概念(1).三个角对应_____、三条边对应_______的两个三角形叫做相似三角形(2).相似三角形的对应角_____,对应边________.(3).相似比等于____的两个三角形全等.问题2:我们已经有哪些判别两三角形相似的方法?(1)交叉型与金字塔形(条件:平行)(2)两角对应相等的两个三角形相似。相等成比例相等成比例1一、复习提问二、探索新知观察图,如果有一点E在边AC上,那么点E应该在什么位置才能使△ADE与△ABC相似呢?31ABAD图中两个三角形的一组对应边AD与AB的长度的比值为.将点E由点A开始=__________.在AC上移动,可以发现当AE=________AC时,△ADE与△ABC相似.此时如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似吗?3131E类比猜想:我们在判断两个三角形全等时,使用了哪些方法?判断三角形相似是否有类似的方法呢?活动一:利用刻度尺和量角器画两个三角形,使它们的两条对应边成比例,并且夹角相等.量一量第三条对应边的长,计算它们的比与前两条对应边的比是否相等.另两个角是否对应相等?你能得出什么结论?ABCDEF如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似.(简单的说成:两边对应成比例且夹角相等的两个三角形相似)证明思路:①①做平行线性质,利用做平行线性质,利用三角形相似性质(三角形相似性质(AAAAAA),),证明三角形证明三角形ADEADE相似于三角形相似于三角形ABCABC。。②②利用利用全等三角形的性质全等三角形的性质,,证明三角形证明三角形ADEADE全等全等于三角形于三角形A′B′C′A′B′C′。。((全等三角形全等三角形ASA)ASA)三角形相似的判定方法2:两边对应成比例且夹角相等的两个三角形相似ABC在△ABC与△DEF中 ∠B=E∠,DEFEFBCDEAB=∴△ABCDEF∽△(两边对应成比例且夹角相等的两个三角形相似)上述判定方法中的“角”一定只能是两对应边的夹角吗?上述判定方法中的“角”一定只能是两对应边的夹角吗?我爱思考想一想:在上述问题中如果这个角是这两条边中其中一条边的对角呢,两个三角形还一定相似吗?GG3.23.2CC3.23.250°)4AB21.650°)EDF两边对应成比例且一边的对角对应相等的两三角形不一定相似两边对应成比例且一边的对角对应相等的两三角形不一定相似例3证明图24.3.7中△AEB和△FEC相似.图24.3.75.1=3654=FEAE5.1=3045=CEBECEBEFEAE=证明 ,∴∴△AEBFEC∽△(如果一个三角形的两条边与另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似). ∠AEB=∠FEC,依据下列各组条件,证明△ABC和△A′B′C′相似∠A=40°,AB=8,AC=15,∠A′=40°,A′B′=16,A′C′=30.1、已知,如图所示,D是△ABC的边AB上的一点,根据下列条件,可证明△ABC∽△ACD的是()A.AC·AB=CA·CDB.BC·AD=CD·ACC.AC2=AB·ADD.CD2=AD·BDABCDCBC·AD=CD·ACAC2=AB·ADCD2=AD·BD证明:∴△ACDABC∽△(两边对应成比例且夹角相等的两个三角形相似).2、如图,D在△ABC的AB边上AD=1,BD=2,AC=.问:△ACD与△ABC相似吗?为什么?3ABCD答:△ACD∽ABC△33=31=ACAD33=ABACABACACAD=∴∠A=A∠ AD=1AC=3BCDEFA3.如果AF×AC=AE×AB,那么相似三角形有()组,分别是————————————ACAB=AEAF或者ACAE=ABAF4、下面图中的两个三角形是否相似?请说说你的理由:4、下面图中的两个三角形是否相似?请说说你的理由:CA455EFB4如果两个三角形的三条边对应成比例,那么这两个三角形相似吗?感觉上应该是能“相似”了.图24.3.8图24.3.8活动二:在图24.3.8的方格上任画一个三角形,再画出第二个三角形,使它的三边长都是原来三角形的三边长的相同倍数.画完之后,用量角器比较两个三角形的对应角,你发现了什么结论?大家的结论都一样吗?我们可以发现这两个三角形相似.如果一个三角形的三条边和另一个三角形的三条边对应成比例,那么这两个三角形似.(简单的说成:三边对应成比例的两个三角形相似)((SSSSSS))CCAABBCC''AA''BB''三边对应成比例的两个三角形相似三边对应成比例的两个三角形相似三角形相似的判...