丁维仲峨边县杨村中心校(垂径定理)VIP免费

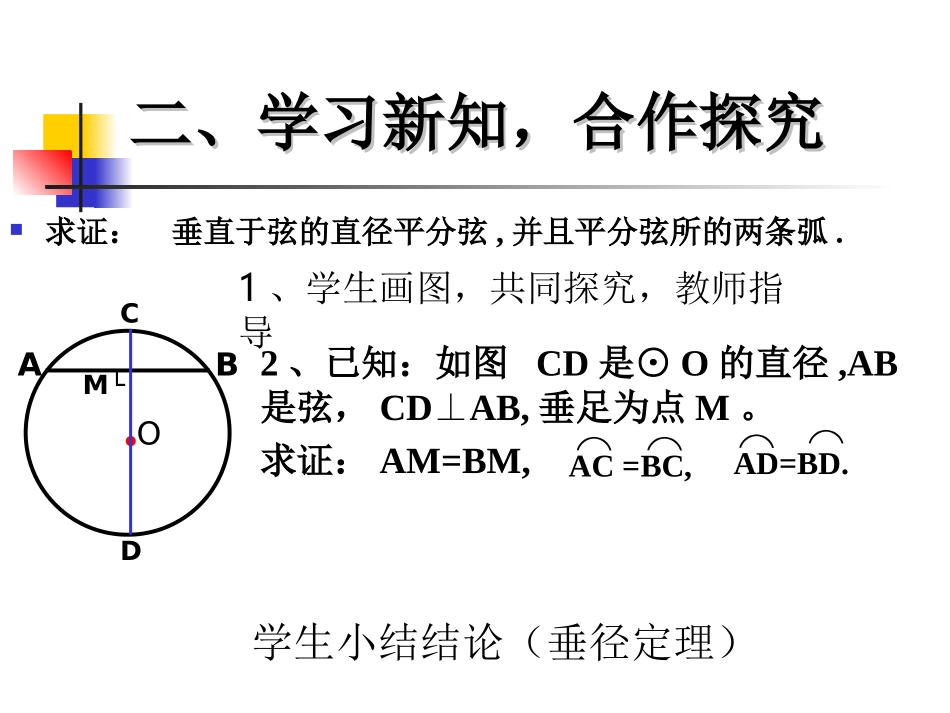
垂径定理峨边县杨村中心校丁维仲③AM=BM,AB是⊙O的一条弦.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.作直径CD,使CDAB,⊥垂足为M.●O下图是轴对称图形吗?如果是,其对称轴是什么?我们发现图中有:ABCDM└由①CD是直径②CDAB⊥可推得⌒⌒④AC=BC,⌒⌒⑤AD=BD.一、复习旧知，导入新知一、复习旧知，导入新知二、学习新知，合作探究二、学习新知，合作探究求证：垂直于弦的直径平分弦,并且平分弦所的两条弧.●OABCDM└2、已知：如图CD是⊙O的直径,AB是弦，CDAB,⊥垂足为点M。求证：AM=BM,⌒⌒AC=BC,⌒⌒AD=BD.1、学生画图，共同探究，教师指导学生小结结论（垂径定理）②CDAB,⊥垂径定理的逆定理:AB是⊙O的一条弦,且AM=BM.你能发现图中有哪些等量关系?与同伴说说你的想法和理由.过点M作直径CD.●O右图是轴对称图形吗?如果是,其对称轴是什么?我们发现图中有:CD由①CD是直径③AM=BM可推得⌒⌒④AC=BC,⌒⌒⑤AD=BD.●MAB┗平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧.你可以写出相应的结论吗?垂径定理的逆定理如图,在下列五个条件中:只要具备其中两个条件,就可推出其余三个结论.●OABCDM└①CD是直径,③AM=BM,②CDAB,⊥⌒⌒④AC=BC,⌒⌒⑤AD=BD.挑战自我填一填1、判断：⑴垂直于弦的直线平分这条弦,并且平分弦所对的两条弧.（）⑵平分弦所对的一条弧的直径一定平分这条弦所对的另一条弧.（）⑶经过弦的中点的直径一定垂直于弦.（）⑷圆的两条弦所夹的弧相等，则这两条弦平行.（）⑸弦的垂直平分线一定平分这条弦所对的弧.（）例1如图，一条公路的转变处是一段圆弧(即图中弧CD,点O是弧CD的圆心),其中CD=600m,E为弧CD上的一点,且OE⊥CD垂足为F,EF=90m.求这段弯路的半径.解:连接OC.●OCDEF┗.)90(,mROFRm则设弯路的半径为,CDOE).(3006002121mCDCF得根据勾股定理,即,222OFCFOC.90300222RR.545,R得解这个方程.545m这段弯路的半径约为1.1300多年前,我国隋朝建造的赵州石拱桥(如图)的桥拱是圆弧形,它的跨度(弧所对是弦的长)为37.4m,拱高(弧的中点到弦的距离,也叫弓形高)为7.2m,求桥拱的半径(精确到0.1m).三、运用新知，自主练习三、运用新知，自主练习赵州石拱桥解：如图，用表示桥拱，所在圆的圆心为O，半径为Rm，经过圆心O作弦AB的垂线OD，D为垂足，与相交于点C.根据垂径定理，D是AB的中点，C是的中点，CD就是拱高.由题设ABABABAB,2.7,4.37CDABABAD21,7.184.3721DCOCOD.2.7R在RtOAD△中，由勾股定理，得,222ODADOA.)2.7(7.18222RR即解得R≈27.9（m）.答：赵州石拱桥的桥拱半径约为27.9m.OABCRD37.47.2四、质疑：同学们通过这节课的学习，还有什么疑问？五、小结：1、定理垂直于弦的直径平分弦,并且平分弦所的两条弧.2、垂径定理的逆定理:平分弦（不是直径）的直径垂直于弦,并且平分弦所对的两条弧.