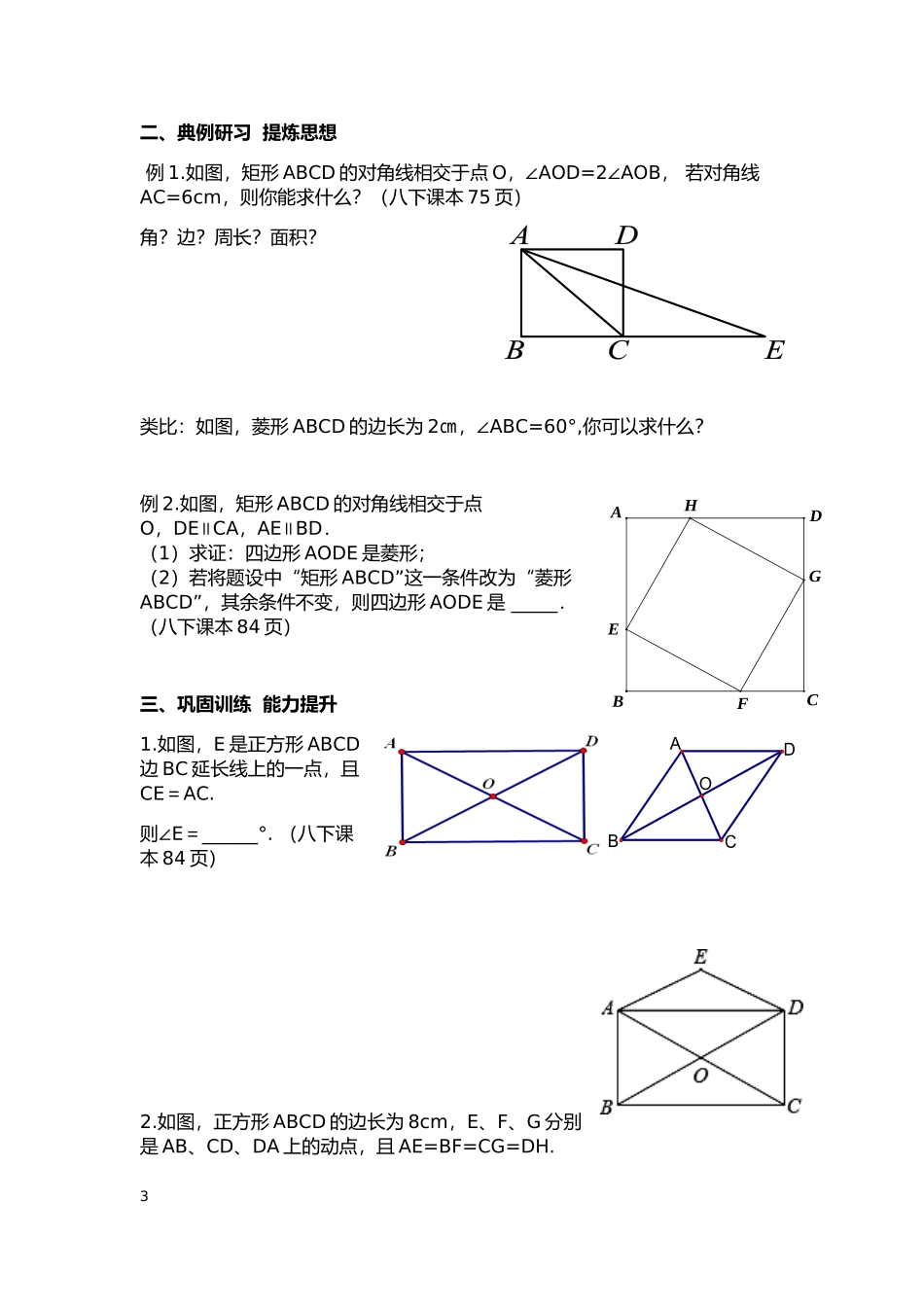
2017年中考数学第一轮复习——矩形、菱形、正方形兴化市昭阳湖初级中学张国金【复习目标】1、掌握矩形,菱形,正方形的概念;2、掌握矩形,菱形,正方形的性质和识别方法;3、掌握矩形,菱形,正方形的对称性,并利用性质解决问题。【本章重点】掌握并会灵活运用特殊平行四边形的定义、性质及判定;会灵活应用特殊平行四边形的相关知识解决一些简单的实际问题。【本章难点】掌握矩形、菱形、正方形的性质及判定条件,以及它们之间存在的联系与区别。【中考透视】中考关于四边形的考题大多结合三角形知识进行考查,而平行四边形及特殊平行四边形的性质是证明两条直线平行、线段相等及角相等的依据.另外关于平行四边形及特殊平行四边形的面积及周长、对称性也常出现在中考题中,这类题有填空题、选择题、计算题和证明题,深刻理解和牢记平行四边形及特殊平行四边形的性质和判定是关键和前提.一、基础训练知识建构1.菱形、矩形、平行四边形、正方形这4种图形中,既是中心对称图形又是轴对称图形的有()个A、1B、2C、3D、42.矩形(菱形)具有而菱形(矩形)不具有的性质有__(填写序号)(1)四条边都相等(2)对角相等(3)对角线相等(4)轴对称图形(5)中心对称图形3、如图,在□ABCD中,可补充条件_________,则四边形ABCD为矩形。变式1:把题设”□ABCD”改为”四边形ABCD”变式2:把结论“矩形”改为“菱形”变式3:把题设”□ABCD”改为”四边形ABCD”同时把结论“矩形”改为“菱形”12017年春学期初三数学一轮复习暨均衡教育课题研讨活动教案考点一:矩形考点二:菱形考点三:正方形2矩形定义有一个角是________的平行四边形叫做矩形矩形的性质对称性矩形是一个轴对称图形,它有________条对称轴矩形还是中心对称图形,它的对称中心就是对角线的交点定理(1)矩形的四个角都是________角(2)矩形的对角线互相平分并且________矩形的判定(1)定义法(2)三个角是直角的四边形是矩形(3)对角线________的平行四边形是矩形拓展(1)矩形的两条对角线把矩形分成四个面积相等的等腰三角形(2)矩形的面积等于两邻边长的积菱形定义有一组________相等的平行四边形叫菱形菱形的性质对称性菱形是轴对称图形,两条对角线所在的直线是它的对称轴菱形是中心对称图形,它的对称中心是两条对角线的交点定理(1)菱形的四条边________(2)菱形的两条对角线互相________平分菱形的判定(1)定义法(2)四边________的四边形是菱形(3)对角线互相________的平行四边形是菱形菱形的面积(1)由于菱形是平行四边形,所以菱形的面积=底×高(2)因为菱形的对角线互相垂直平分,所以其对角线将菱形分成4个全等三角形,故菱形的面积等于两对角线乘积的________正方形的定义有一组邻边________,且有一个角是________的平行四边形叫做正方形正方形的性质(1)正方形的对边________(2)正方形的四边________(3)正方形的四个角都是________(4)正方形的对角线相等,互相________(5)正方形既是轴对称图形也是中心对称图形,对称轴有________条,对称中心是对角线的交点正方形的判定(1)定义法(2)有一组邻边相等的矩形是正方形(3)有一个角是直角的菱形是正方形(4)既是矩形又是菱形的四边形是正方形二、典例研习提炼思想例1.如图,矩形ABCD的对角线相交于点O,∠AOD=2∠AOB,若对角线AC=6cm,则你能求什么?(八下课本75页)角?边?周长?面积?类比:如图,菱形ABCD的边长为2㎝,∠ABC=60°,你可以求什么?例2.如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.(1)求证:四边形AODE是菱形;(2)若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形AODE是_____.(八下课本84页)三、巩固训练能力提升1.如图,E是正方形ABCD边BC延长线上的一点,且CE=AC.则∠E=______°.(八下课本84页)2.如图,正方形ABCD的边长为8cm,E、F、G分别是AB、CD、DA上的动点,且AE=BF=CG=DH.3ODABCFGHBADCE(八下课本82页)(1)求证:四边形EFGH是正方形;(2)判断直线EG是否经过某一定点,说明理由;(3)求四边形EFGH面积的最小值.四、课堂小结交流感悟本节课你收获了哪些知识?掌握了哪些解题方法?领悟了哪些数学思想?五、课后作业,巩固提高必做题:《初中毕业升学考试指导》P109-111选做题:《初中毕业升学考试指导》P112-1134