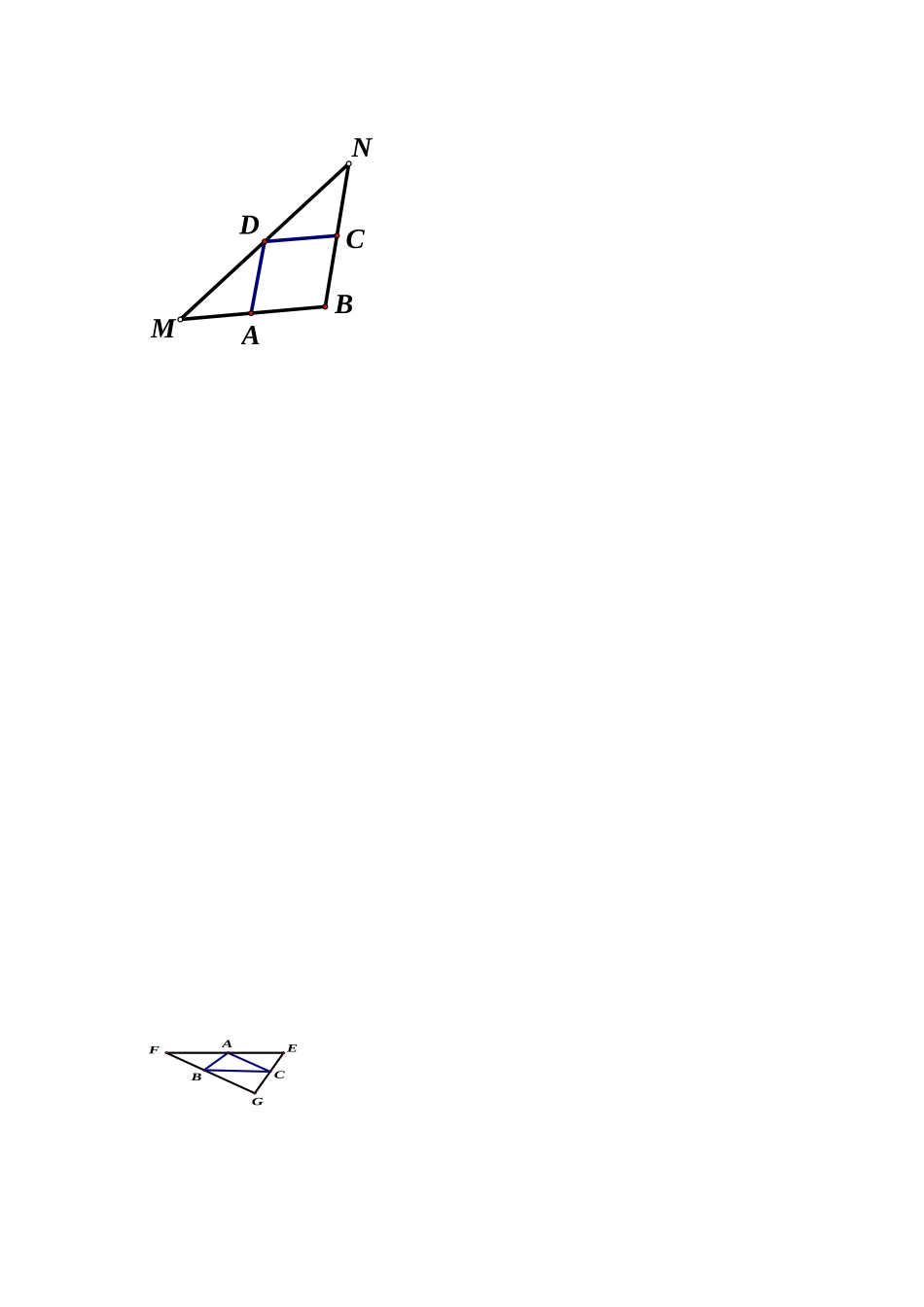
ABCD平行四边形及其性质(1)教学目的:1.掌握平等行四边形的概念、性质及其应用;2.掌握平行线间的距离概念3..知道解决平行四边形问题的基本思想是化为三角形问题来解决,渗透转化思想。教学重点:平行四边形的概念及性质教学难点:平行四边形的概念及性质的灵活运用教学过程:同学们,走进数学,我们已经认识了多种平面图形,比如平行线,全等三角形和四边形等,它们使我们的生活更加多姿多彩。本章我们将一起对特殊四边形进行探究。一、利用分类、特殊化的方法引出平行四边形的概念1、生准备两个全等三角形,学生动手操作。提问:(1)用两个全等的三角形能拼出多少个不同的四边形?(多媒体展示所有拼法)(2)这些四边形中有几个特殊四边形?这几个特殊四边形的两组对边有什么特殊位置关系?说说你的理由2、对比引出平行四边形的概念(1)引导学生根据图形叙述平行四边形的概念,引出课题平行四边形定义:两组对边分别平行的四边形是平行四边形。使用方法:四边形ABCD是平行四边形AD∥BC,AB∥CD(平行四边形的定义)反之AD∥BC,AB∥CD四边形ABCD是平行四边形(平行四边形的定义)(2)平行四边形的符号表示方法:ABCD师多媒体展示生活中的平行四边形,体会数学在生活中的作用。二、探索平行四边形的性质及其证明1.利用拼得的平行四边形从边、角的位置关系及数量关系入手,观察猜想平行四边形的性质如下:(1)边:①对边平行(定义),②对边相等(性质定理2)如图:AD=BC,AB=CD且AD∥BC,AB∥CD2.师问:如何验证你的猜想?(因为拼出四边形的两个三角形全等)3、性质的证明.如图添加一条对角线,将四边形分割成两个三角形,利用全等三角形知识证出性质证明过程:已知,四边形ABCD是平行四边形求证:∠B=∠D,∠BAD=∠DCB,AD=BC,AB=CD证明:连结BD∵四边形ABCD是平行四边形∴AD∥BC,AB∥CD∴∠ADB=∠CBD,∠ABD=∠CDB∴∠ADC=∠CBA∵DB=BD∴△ABD≌△CDB(ASA)∴A=∠C,AD=BC,AB=CD(由学生完成)性质的应用:如图∵四边形ABCD是平行四边形不转化为三角形能证明平行四边形的对角相等吗ABCDFEADBCCBAD∴①AB∥,AD∥②AB=,=③∠B=∠,∠A=∠练习:⑴若∠A=130°,则∠B=∠c=∠D=若AB=1,BC=2,则ABCD的周长=例题教学:如图,平行四边形ABCD中,DE⊥AB于点E,BF⊥CD于点F.求证:AE=CF师问:DE=DF吗?如下图,AC//BD,垂线段AB=CD吗?给出平行线间的距离的概念学以致用:1.如图,ABCD中,CD=5,BC=9,BE平分∠ABC,求DE变式:若CF平分∠BCD交AD于点F,求EF的长三、小结这节课你有哪些收获,和老师同学交流一下1、定义:两组对边分别平行的四边形叫做平行四边形.2、性质:平行四边形的对边平行。平行四边形的对边相等。平行四边形的对角相等。3、平行线间的距离4.性质的运用四.课堂小测:ABCD中:1.小明想用18m的绳子围成一个邻边相差1m平行四边形,它的边长分别为.2.若∠A+∠C=200°,则∠A=∠B=.3.若AB:BC=3:4,周长为14,则CD=DA=.4.若AC⊥AB于点A,且AB=3,AC=4,则平行四边形ABCD的周长是面积是五、作业1.如图,△ABC中,AB//EG,EF//BC,AC//FG,则图中有个平行四边形2.ABCD中,如果∠B的外角是50°,∠A=度,∠C=°,∠D=°3、ABCD的周长为40cm,⊿ABC的周长为25cm,则对角线AC长为()4.如图在△MNB中,BN=6,点A,C,D分别在MB,NB,MN上,四边形ABCD为平行四边形,且∠NDC=∠MDA,求四边形ABCD的周长EFEGBCANDBMAC