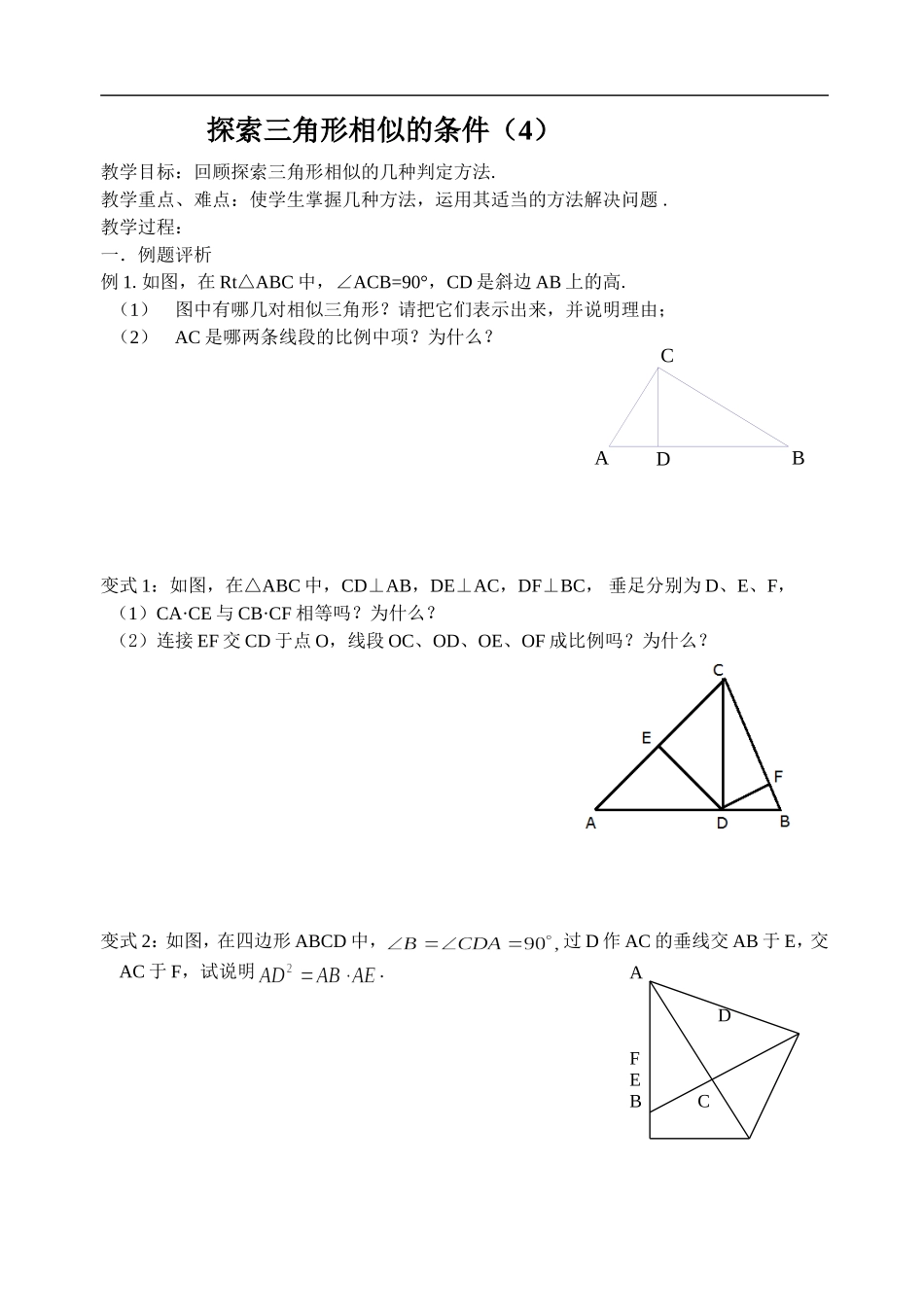
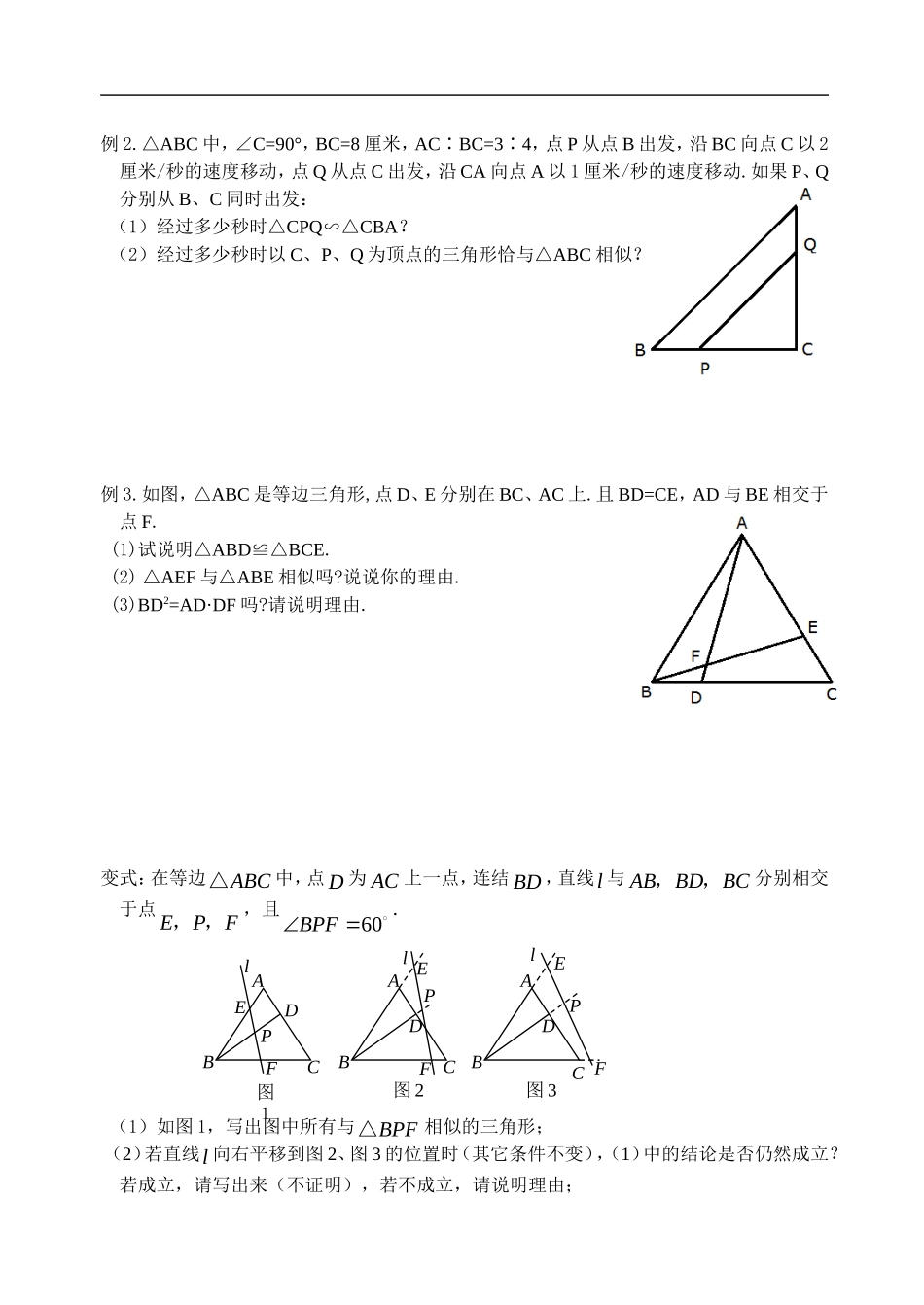
探索三角形相似的条件(4)教学目标:回顾探索三角形相似的几种判定方法.教学重点、难点:使学生掌握几种方法,运用其适当的方法解决问题.教学过程:一.例题评析例1.如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高.(1)图中有哪几对相似三角形?请把它们表示出来,并说明理由;(2)AC是哪两条线段的比例中项?为什么?变式1:如图,在△ABC中,CD⊥AB,DE⊥AC,DF⊥BC,垂足分别为D、E、F,(1)CA·CE与CB·CF相等吗?为什么?(2)连接EF交CD于点O,线段OC、OD、OE、OF成比例吗?为什么?变式2:如图,在四边形ABCD中,过D作AC的垂线交AB于E,交AC于F,试说明.DCBAADFEBC例2.△ABC中,∠C=90°,BC=8厘米,AC∶BC=3∶4,点P从点B出发,沿BC向点C以2厘米/秒的速度移动,点Q从点C出发,沿CA向点A以1厘米/秒的速度移动.如果P、Q分别从B、C同时出发:(1)经过多少秒时△CPQ∽△CBA?(2)经过多少秒时以C、P、Q为顶点的三角形恰与△ABC相似?例3.如图,△ABC是等边三角形,点D、E分别在BC、AC上.且BD=CE,AD与BE相交于点F.(1)试说明△ABD≌△BCE.(2)△AEF与△ABE相似吗?说说你的理由.(3)BD2=AD·DF吗?请说明理由.变式:在等边ABC△中,点D为AC上一点,连结BD,直线l与ABBDBC,,分别相交于点EPF,,,且60BPF.(1)如图1,写出图中所有与BPF△相似的三角形;(2)若直线l向右平移到图2、图3的位置时(其它条件不变),(1)中的结论是否仍然成立?若成立,请写出来(不证明),若不成立,请说明理由;ABCFDP图3ABCDP图2EllEFABCDP图1lEFFDECBA课后练习:姓名1.如图,要使△ABC∽△BCD,必须具备的条件是()A.=B.=C.BC2=AC·DCD.BD2=DA·DC2.下列说法①凡正方形都相似;②凡等腰三角形都相似;③凡等腰直角三角形都相似;④直角三角形斜边上的中线与斜边的比为1∶2;⑤两个相似多边形的面积比为4∶9,则周长的比为16∶81.中,正确的个数有()A.1B.2C.3D.43.如图,D、E是ΔABC的边AB、AC上的点,DE与BC不平行,请填上一个你认为合适的条件:,使得ΔADE∽ΔACB.4.已知:ΔABC,P是边AB上的一点,连结CP.(1)当∠ACP满足条件时,ΔACP∽ΔABC.(2)当AC:AP=时,ΔACP∽ΔABC.5.若AB∥CD∥EF,则图中相似的三角形有对.第3题图.6.如图,P是RtΔABC的斜边BC上异于B、C的一点,过点P作直线截ΔABC,使所截得的三角形与ΔABC相似满足这样条件的直线最多能作出条.第1题图第4题图第5题图第6题图7.如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF=CD,下列结论:①∠BAE=30°,②AE⊥EF,③△ABE~△AEF,④△ADF~△ECF,⑤AF=AB+FC,其中正确的结论的个数为.第7题图8.如图:△PCD是正三角形,∠APB=120°.试证明,△APC∽△PBD.9.在正方形ABCD中,AB=2,P是BC边上与B、C不重合的任意点,DQ⊥AP于Q.(1)求证:ΔDQA∽ΔABP.DCBA(2)当P点在BC上变化时,线段DQ也随之变化.设PA=x,DQ=y,求y与x之间的函数关系.10.已知,如图,CD是Rt△ABC斜边上的中线,DE⊥AB交BC于F,交AC的延长线于E,求证:(1)△ADE∽△FDB;(2)CD2=DE·DF.11.如图所示,在ΔABC中,BA=BC=20cm,AC=30cm,点P从A点出发,沿着AB以每秒4cm的速度向B点运动;同时点Q从C点出发,沿CA以每秒3cm的速度向A点运动,设运动时间为x.(1)当x为何值时,PQ∥BC?(2)当,求的值;(3)ΔAPQ能否与ΔCQB相似?若能,求出AP的长;若不能,请说明理由.