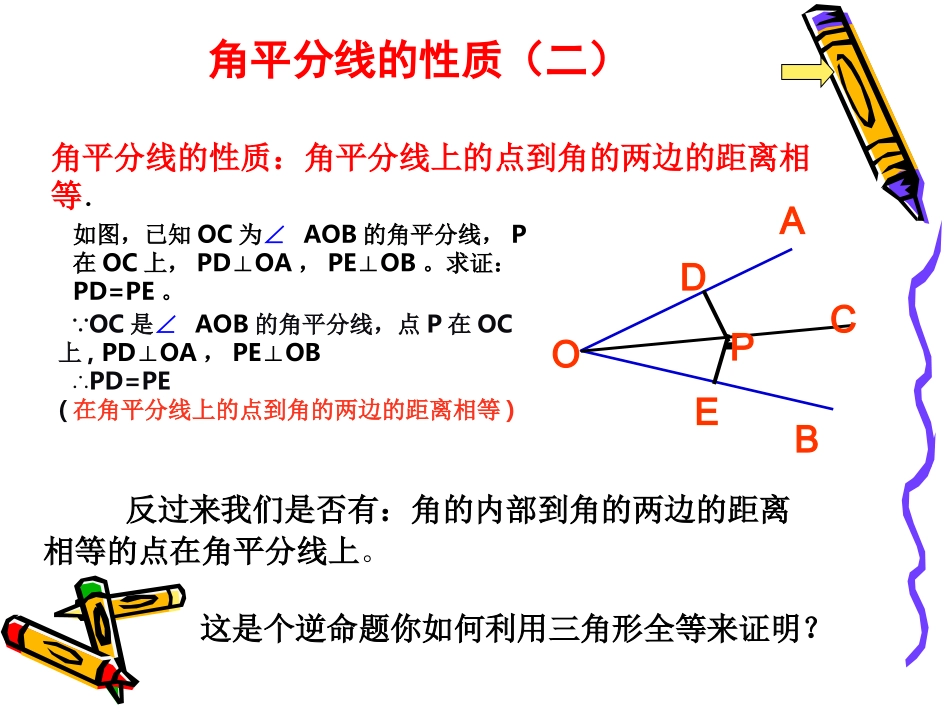
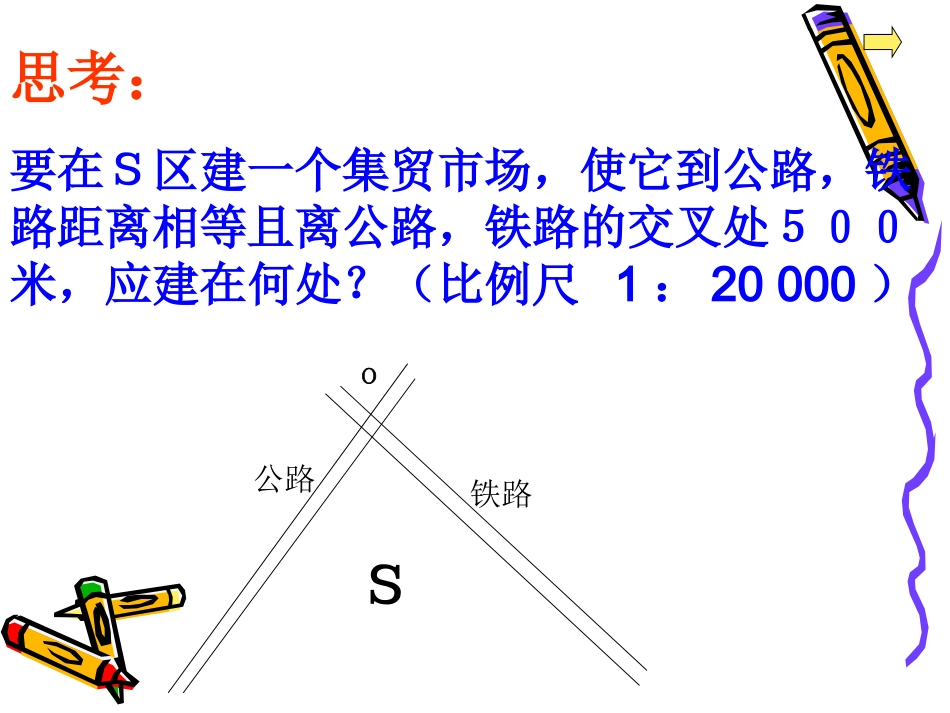
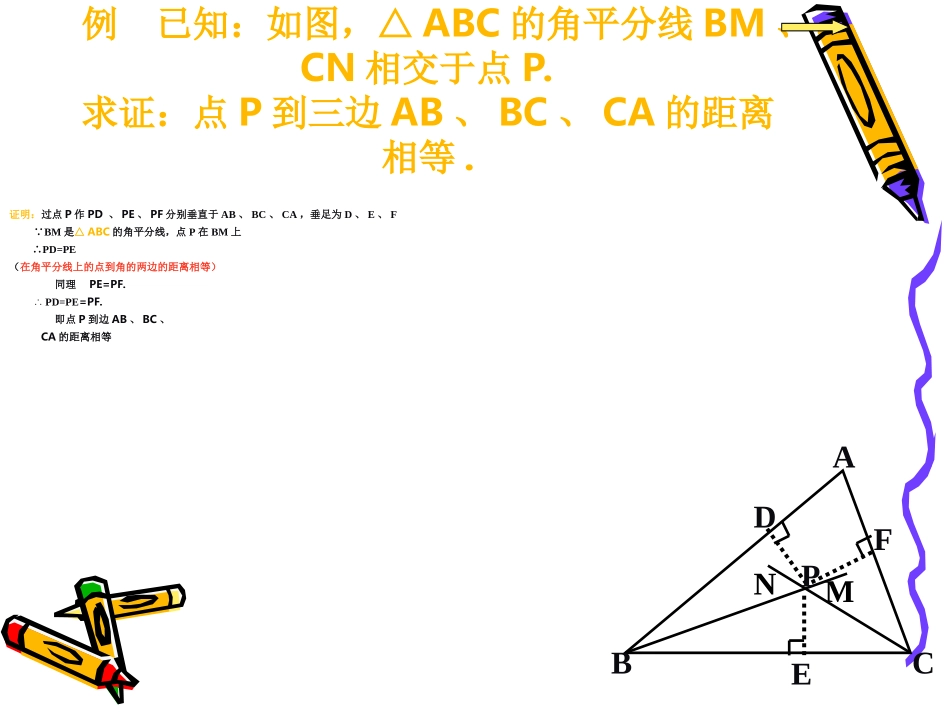
角平分线的性质(二)角平分线的性质:角平分线上的点到角的两边的距离相等.反过来我们是否有:角的内部到角的两边的距离相等的点在角平分线上。这是个逆命题你如何利用三角形全等来证明?如图,已知OC为∠AOB的角平分线,P在OC上,PD⊥OA,PE⊥OB。求证:PD=PE。BOAC·DPE∵OC是∠AOB的角平分线,点P在OC上,PD⊥OA,PE⊥OB∴PD=PE(在角平分线上的点到角的两边的距离相等)思考:要在S区建一个集贸市场,使它到公路,铁路距离相等且离公路,铁路的交叉处500米,应建在何处?(比例尺1:20000)SO公路铁路例已知:如图,△ABC的角平分线BM、CN相交于点P.求证:点P到三边AB、BC、CA的距离相等.证明:过点P作PD、PE、PF分别垂直于AB、BC、CA,垂足为D、E、F∵BM是△ABC的角平分线,点P在BM上∴PD=PE(在角平分线上的点到角的两边的距离相等)同理PE=PF.∴PD=PE=PF.即点P到边AB、BC、CA的距离相等DEFABCPMN练习:如图,△ABC的∠B的外角的平分线BD与∠C的外角的平分线CE相交于点P.求证:点P到三边AB,BC,CA所在直线的距离相等.ABCDEPFGHBP1:画一个已知角的角平分线;及画一条已知直线的垂线;2:角平分线的性质:角的平分线上的点到角的两边的距离相等.3:角平分线的判定结论:到角的两边的距离相等的点在角平分线上。