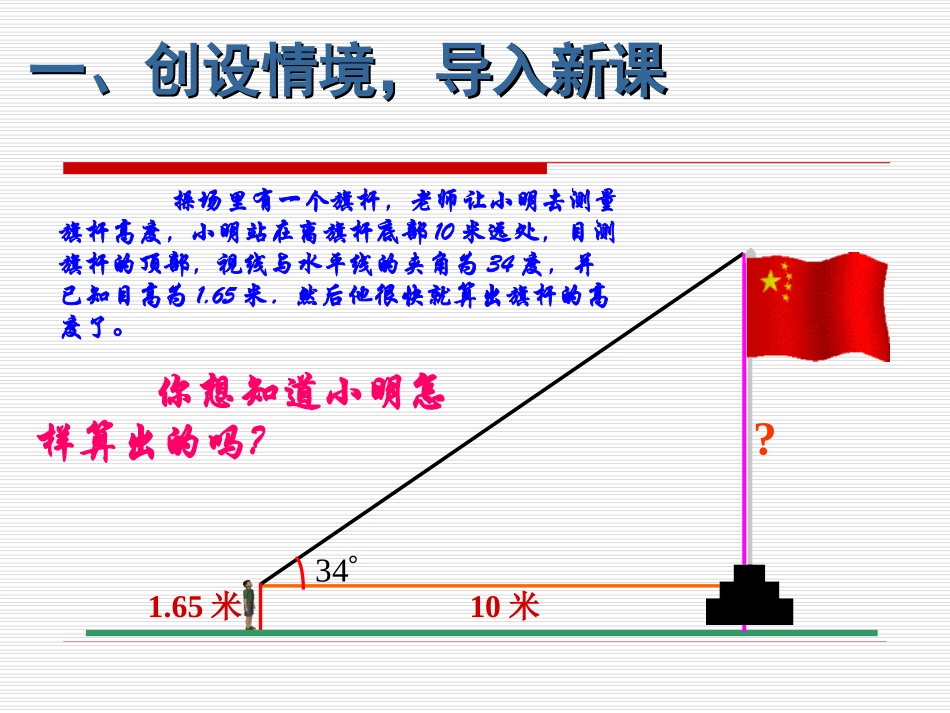
操场里有一个旗杆,老师让小明去测量旗杆高度,小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为34度,并已知目高为1.65米.然后他很快就算出旗杆的高度了。1.65米3410米?你想知道小明怎样算出的吗?一、创设情境,导入新课一、创设情境,导入新课二、探究新知,建立模型二、探究新知,建立模型为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌.现测得斜坡与水平面所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?ACB在Rt△ABC,∠A=30°,BC=35°,求AB的长.根据“在直角三角形中,30°角所对的边等于斜边的一半”,即21ABBCA斜边的对边可得AB=2BC=70m,也就是说,需要准备70m长的水管.二、探究新知,建立模型二、探究新知,建立模型35m30°?想一想:你能用数学语言来表述这个实际问题吗?在上面的问题中,如果使出水口的高度为50m,那么需要准备多长的水管?结论:在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于21ABC50m30m,21'''ABCBA斜边的对边B'C'AB'=2B'C'=2×50=100分析:在Rt△ABC中,∠C=90°,由于∠A=45°,所以Rt△ABC是等腰直角三角形,由勾股定理得22222BCBCACABBCAB222212BCBCABBC因此结论:在直角三角形中,当一个锐角等于45°时,不管这个直角三角形的大小如何,这个角的对边与斜边的比都等于22如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比,你能得出什么结论?ABBCABC猜想在一个直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,它的对边与斜边的比是否也是一个定值?探究任意画一个RtRt△△ABCABC和和RtRt△△A′B′C′A′B′C′,,使得∠使得∠CC==∠∠C′C′=90°=90°,∠,∠AA==∠∠A′A′==αα,那么与有什么关,那么与有什么关系,你能解释一下吗?系,你能解释一下吗?ABBCABBCC′A′B′ACB定义:在Rt△Rt△ABCABC中,∠∠CC=90°=90°,我们把锐角A的对边与斜边的比叫做∠∠AA的的正弦正弦,记作,记作sinA,即.sincaAA斜边的对边例如:当∠∠AA=30°=30°时,我们有时,我们有例如:当∠∠AA=45°=45°时,我们有时,我们有;2130sinsinA.2245sinsinA注意:(1)sinA是一个完整的符号,它表示∠A的正弦函数,一般简单地叫∠A的正弦。记法里习惯省去角的符号“∠”;(2)sinA没有单位,它表示一个比值,即直角三角形中∠A的对边与斜边的比;sinA不表示“sin”乘“A”;ABC斜边c对边ab例:如图,在RtRt△△ABCABC中,∠∠CC=90°=90°,求sinA和sinB的值.ABCABC34513分析:求sinA,就要先知道∠∠AA的对边与斜边的值,求sinB,就要先知道∠∠BB的对边与斜边的值,而直角三角形边的问题往往又涉及勾股定理的应用.三、解析、应用与拓展三、解析、应用与拓展练一练1判断对错A10m6mBC1)如图(1)sinA=()(2)sinB=()(3)sinA=0.6m()(4)SinB=0.8()ABBCBCAB√√××sinA是一个比值,无单位2)如图,sinA=()BCAB×在Rt△ABC中,锐角A的对边和斜边同时扩大100倍,sinA的值()A.扩大100倍B.缩小C.不变D.不能确定C1100练一练2练一练3根据右图,求sinA和sinB的值.BAC351.本节课你学到了什么数学知识?2.你还有什么困惑?四、小结归纳四、小结归纳1.必做题:2.选做题:五、布置作业五、布置作业(1)在Rt△ABC中,sinA=,AB=10,求BC的长.(2)如下图所示,菱形的两条对角线长分别是16和12.较长的一条对角线与菱形的一边的夹角为θ,求sinθ的值.ABCDOθ教材82页习题28.1第1题和第4题(只求正弦值).谢谢大家!