第1章复习与小结VIP免费

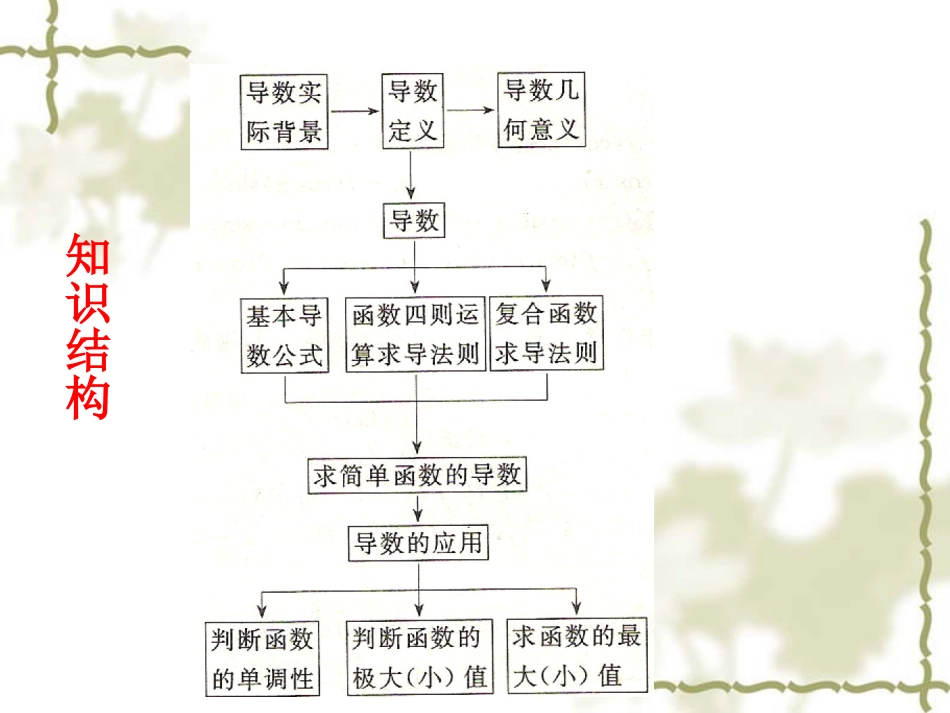
高中数学高中数学选选修修2-22-2高中数学高中数学选选修修2-22-2主要题型1．以填空、选择考查导数的概念，求函数的导数，求函数的极、最值．2．与导数的几何意义相结合的函数综合问题，利用导数证明函数的单调性或求函数的单调区间，多为中档题．3．利用导数求实际问题中的最值问题，为中档偏难题．知识结构.________22,1.12处的瞬时变化率为则上一点，）是曲线（已知点PxyP.________3142.23的倾斜角为）处的切线，在点（曲线xxy数学应用.425.1平行的切线的方程与直线求曲线例xyxy.025816)1625(2425.425162522542.25550000000yxxyyxxxyxyxyyxxyxx即，因此，所求切线方程为，，所以平行，因为所求切线与直线，得由），上的点（解：设所求切线过曲线变式：求过点A的切线方程？.)2,1(2.23的切线方程处，求在点和点：已知曲线例AAxxyC.2)1(222)1(13)(2xyxyfkxxf即所求的切线方程为：，解：.094)1(412212)1(2212110)12(1)1)(13()2(22,1))(13()2(13)()2(00000200200300200302000300yxxyxxyxyxxxxxxxxxAxxxxxyxxfkxxxP，即时，所求切线方程为当；，即时，所求切线方程为当或解得）化简得（）（切线过点又切线方程为，则，解：设切点为点评:“过某点”与“在某点处”是不同的，故审题应细.1.用公式法求下列导数：2)13(2)1(xxyxeyxcos)2(2)1(log)4(23xy2)13(622)13(3)13(22)13()2(2112221xxxxxxxxy）解：（xxxxxxxysincos1)sin(sin1)3(xexeyxxsincos2)2(221log2)1(log11)4(23232xexxexy)sinln()3(xxy._____)0()1(32)(.22ffxxxf，则已知.6)0(64)(2)1()1(34)1()1(34)(fxxfffffxxf，，，解：由已知得321.()31.Rfxaxxxa函数在上是减函数，求的取值范围导数的应用2.函数f(x)=ax3+x+1有极值的充要条件是（）A．a>0B．a≥0C．a<0D．a≤03.已知函数f(x)＝x3-3ax2+2bx在点x＝1处有极小值－1，试确定a，b的值，并求出f(x)的单调区间.略解：单增区间为（－∞，－）和（1，＋∞）单间区间为（－，1）．(1)1(1)01132fabf＝－＝，＝＝1313分析：f(x)在x＝1处有极小值－1，意味着f(1)＝－1且f’(1)＝0，故取点可求a，b的值，然后根据求函数单调区间的方法，求出单调区间..2312)()1(:ln)(.4的值求实数，上的最小值为，）若函数在（的单调区间；函数求，已知函数aexfxaxxf课本P56复习题．回顾小结课外作业导数的概念、几何意义、运算及其在函数研究中的作用．