第2讲：图形表示VIP免费

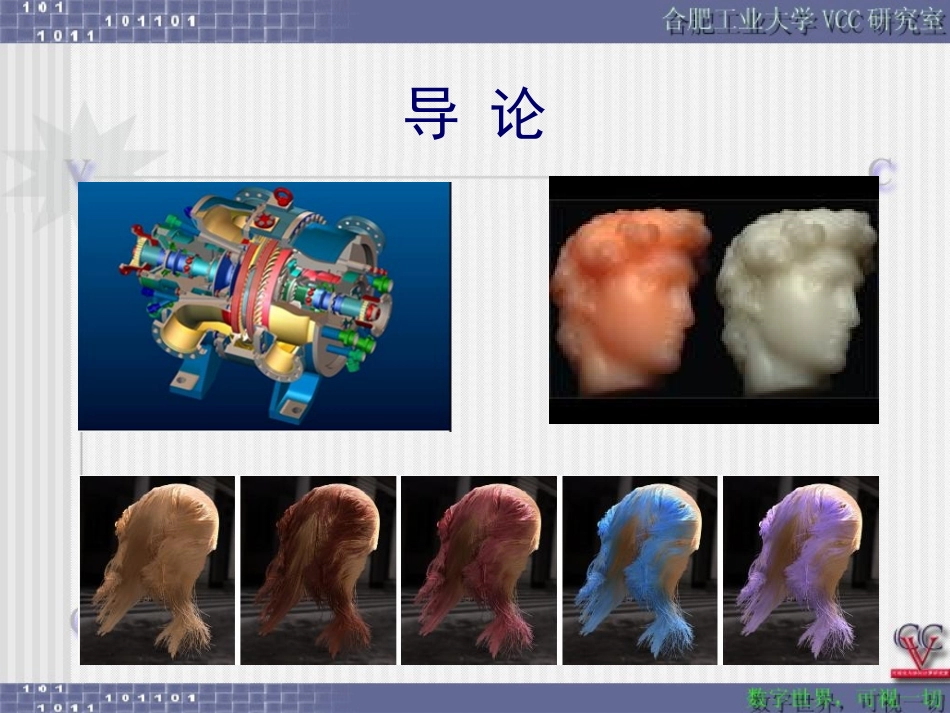
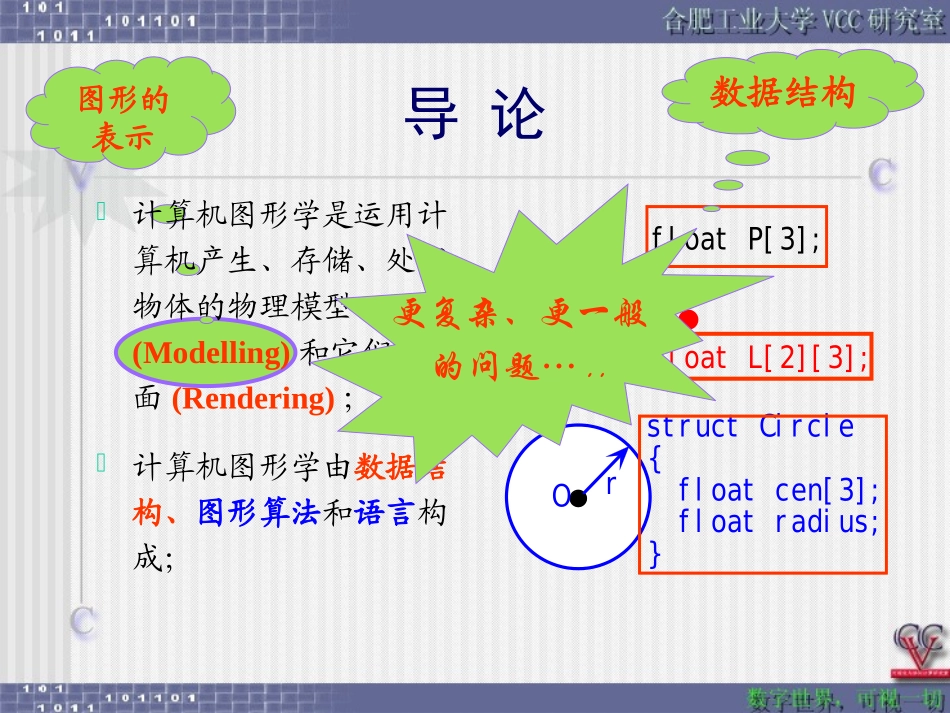
第2讲：图形的表示罗月童合肥工业大学，VCC研究室Cadcg.hfut.edu.cn导论图形的表示导论计算机图形学是运用计算机产生、存储、处理物体的物理模型(Modelling)和它们的画面(Rendering)；计算机图形学由数据结构、图形算法和语言构成；floatP[3];SEfloatL[2][3];OrstructCircle{floatcen[3];floatradius;}数据结构更复杂、更一般的问题…..目录基本几何元素的表示三维形体的表示相关概念拓扑信息+几何信息正则几何运算欧拉公式小结基本图形元素与段的概念µãÏßÌåÃæ»·基本几何元素的表示（数学意义上的）µãÏßÌåÃæ»·点µã0()(),()xxtyytzzttt0维几何元素点是形体中的最基本的元素，自由曲线、曲面或其他形体均可用有序点集表示。用计算机存储、管理、输出形体的实质就是对点集及其连接关系的管理；线、面Ïß0,()(),()1xxtyytzzttÃæ(,)(,),(,)0,10,1xxuvyyuvzzuvuv三维形体体是三维几何元素，由封闭表面围成空间，是欧式空间中非空、有界的封闭子集；其边界是有限面的集合；环»·环是有序、有向边组成的面的封闭边界；外环：按逆时针排序内环：按顺时针排序属性：有且仅有一个外环0到n个内环小测试：几维曲线？目录基本几何元素的表示三维形体的表示相关概念拓扑信息+几何信息正则几何运算欧拉公式小结三维形体体是三维几何元素，由封闭表面围成空间，是欧式空间中非空、有界的封闭子集；其边界是有限面的集合；•指出“应该这样，应该那样….”——缺乏可操作性•没说“怎样才能这样，怎样才能那样……”——具体实现方法三维形体的表示ʵÌåÄ£ÐÍÏß¿òÄ£ÐͱíÃæÄ£ÐÍ没有绝对的“好”与“坏”，但适用的场合不同线框模型：顶点及边的集合结构简单，易于处理！缺点之一：存在视觉二义性ABA和B，谁到你更近？缺点之二：不能表示曲面顶点在哪？边在哪？近似表示线框模型采用顶点及边的集合来描述优点：数据结构简单处理容易缺点：不能表示含有曲面的物体点和边信息容易出现二义性三维形体的表示ʵÌåÄ£ÐÍÏß¿òÄ£ÐͱíÃæÄ£ÐÍ没有绝对的“好”与“坏”，但适用的场合不同表面模型：面的集合4个平面1个球面表面模型：广泛应用应用于“看看就够”的场合，如游戏、电影、漫游等表面模型：研究众多模型化简模型分割模型变形不仅仅为了“看看”•要用多少吨钢材？•力学：能否承重？•热工：能否抗高温？•能否抗几级地震？•……实体模型实体模型：完全真实的表示点P和三维形体B之间：内部外部边界上内部外部边界线框模型否否否表面模型否否是实体模型是是是三维形体线框模型实体模型表面模型空间分割构造实体边界表示空间分割：枚举法000000100000110000111011111111111000ö¾Ù±íʾ·¨空间分割：枚举法的变种数据量大数组不同分辨率八叉树四（八）叉树图4-30二维平面图形对象的四叉树表示BBEFB1234BBBEBBBBFBFEFEEEFEEFFEFFFFFEEEF象限2象限3象限4象限1......(a)(b)构造实体几何表示法（CSG—ConstructiveSolidGeometry）ÇòS......ÖùC......*SC?构造实体几何表示法*ÇòÖù构造实体几何法构造实体几何法（CSG—ConstructiveSolidGeometry）用一棵二叉树来描述：根节点：实体叶子节点：基本体素中间节点：正则集合算子扩展：包含几何变换另一种构造：扫描表示也称扫掠表示,可以利用简单的运动规则生成有效实体基本原理：将一个点、一条边、一个面沿某一路径扫描时，所形成的轨迹将定义一个一维的、二维的、或三维的实体边界表示法判断准则：对确定点P，能否确定：P在实体内部P在实体的边界上P在实体外部记录信息：边界面边界的方向边界表示法描述实体描述边界面面的形状面的边界面的方向边的形状边的边界边的方向起点终点多边形表面模型ABCDVABCABDBCDACDABBCCAADBDCDABCD¶¥µã±íAx1,y1,z1Bx2,y2,z2Cx3,y3,z3Dx4,y4,z4±ß±íABA,BBCB,CCAC,AADA,DBCB,CCDC,D¶à±ßÐαíABCAB,BC,ACABDAB,BD,ADBCDB...