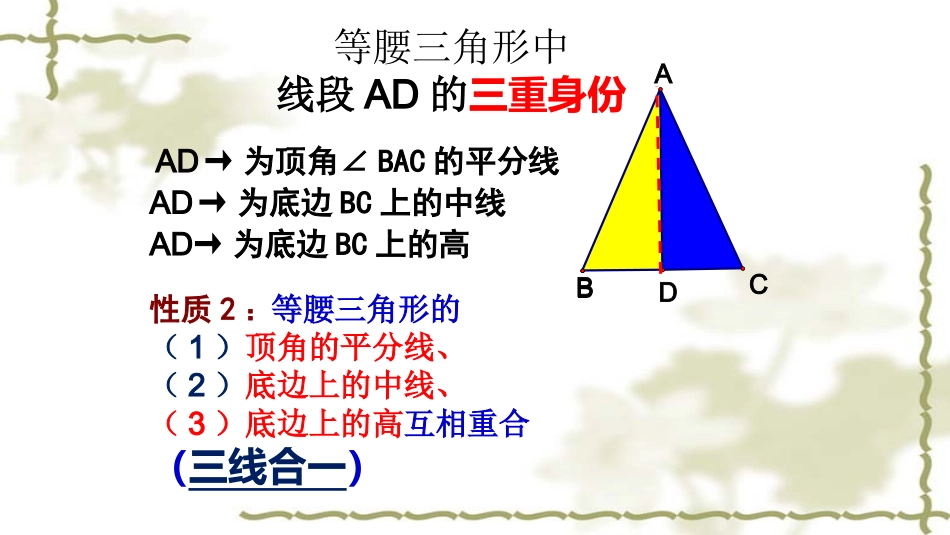
三线合一的简单运用单位:鄱阳县湖城学校执教:邱君新人教版八年级上册①AB=AC②BD=CD③∠BAD=∠CAD④∠ADB=∠ADC=90度BACD把等腰三角形沿折痕对折,发现其中重合的线段和角.重合的线段:重合的角:AD→为底边BC上的中线AD→为顶角∠BAC的平分线AD→为底边BC上的高等腰三角形中线段AD的三重身份DBCAB性质2:等腰三角形的(1)顶角的平分线、(2)底边上的中线、(3)底边上的高互相重合(三线合一)①AB=AC或(∠B=∠C)②∠BAD=CAD∠③ADBC⊥④BD=CDABDC在△ABC中,对于以下四个条件根据轴对称和全等知识我知道四个条件知道任意两个可以退出其它两个。这就是知二推二三线合一的知二推二三线合一的简单应用1.如图,已知AB=BC,D是AC的中点,∠A=34°,则∠DBC=度.56因为AB=BC,D是AC的中点所以BD平分∠ABC,BDAC⊥∠ABD=90°-∠A=90°-34°=56°∠ABD=∠DBC=56°知道等腰和中线推高和角平分线2.⊿ABC中,AD平分∠BAC,DE⊥AB于E,DFAC⊥于F,试说明:EFAD⊥。ABCDEFG知道等腰和角平分线推高∵∠1=2∠DE⊥AB,DFAC⊥∴DE=DF,又AD公共∴△AEDADF(HL)≌△故AE=AF213.如图,∠A=D=90°,AB=CD∠,AC与BD相交于点F,E是BC的中点.求证:∠BFE=CFE.∠证明:∵∠1=2∠(对顶角相等)∠A=D=90°∠AB=CD∴△ABFDCF≌△(AAS)∴BF=CF∴△BCF是等腰三角形.又E是BC的中点,∴EF是∠BFC的角平分线.∴∠BFE=CFE.∠()三线合一知道等腰和中线推角平分线4.已知:如图,在△ABC中,AD平分∠BAC,CDAD,D⊥为垂足,AB>AC。求证:∠2=1+B∠∠ABCED213延长CD与AB相交于点E因为∠EAD=CAD,CDAD∠⊥所以AE=AC,则∠2=3∠故∠3=1+B∠∠则∠2=1+B∠∠知道角平分线和高推等腰