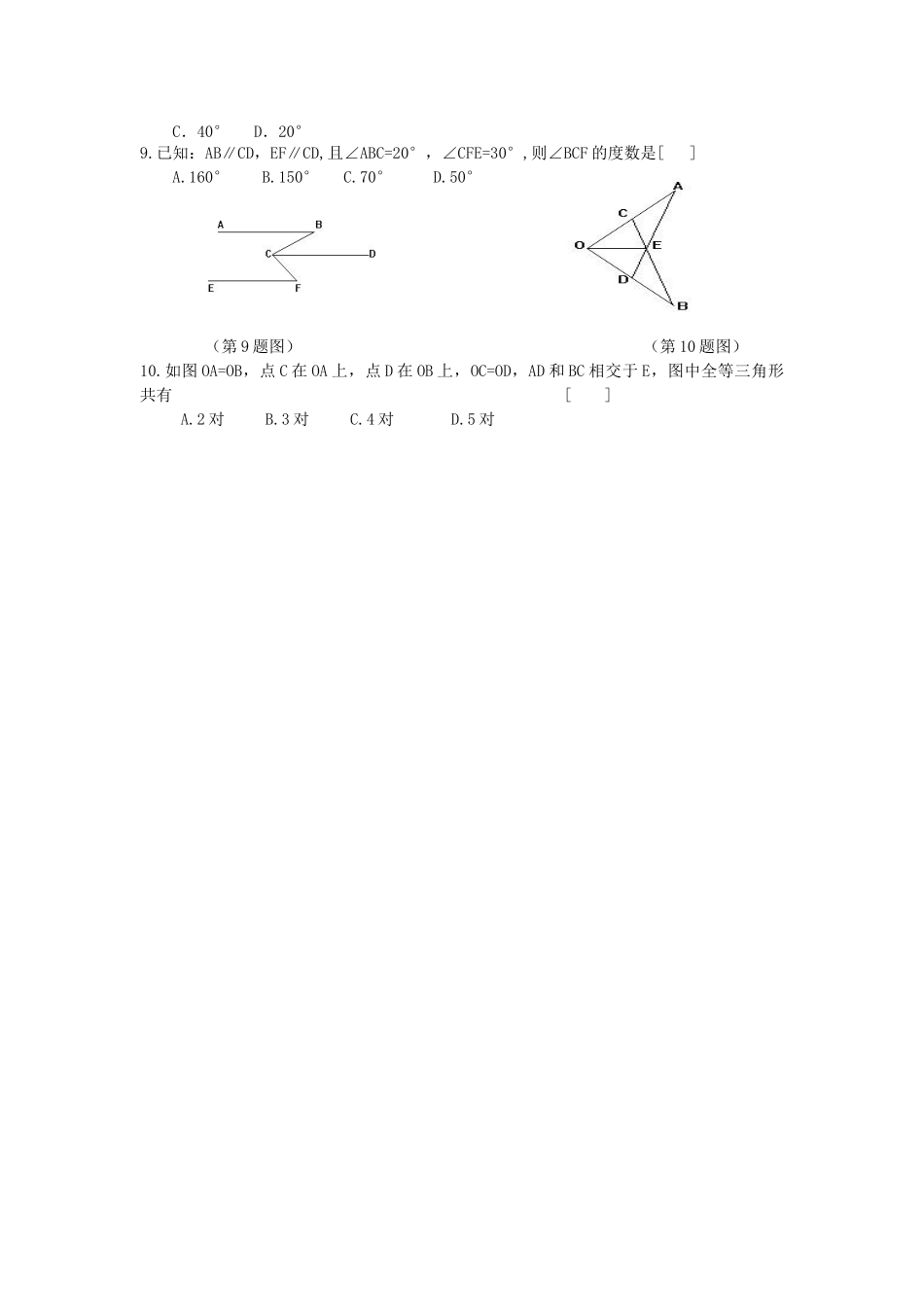
ABCDEEBACBAMCDM图3图4图1图2初中几何综合复习练习题及答案学校姓名一、典型例题例1(2005重庆)如图,在△ABC中,点E在BC上,点D在AE上,已知∠ABD=∠ACD,∠BDE=∠CDE.求证:BD=CD。例2(2005南充)如图2-4-1,⊿ABC中,AB=AC,以AC为直径的⊙O与AB相交于点E,点F是BE的中点.(1)求证:DF是⊙O的切线.(2)若AE=14,BC=12,求BF的长.例3.用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.(1)用这两部分纸片除了可以拼成图2中的Rt△BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.(2)若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程01)1(2mxmx的两个实数根,试求出原矩形纸片的面积.二、强化训练练习一:填空题1.一个三角形的两条边长分别为9和2,第三边长为奇数,则第三边长为.2.已知∠a=60°,∠AOB=3∠a,OC是∠AOB的平分线,则∠AOC=___.3.直角三角形两直角边的长分别为5cm和12cm,则斜边上的中线长为4.等腰Rt△ABC,斜边AB与斜边上的高的和是12厘米,则斜边AB=厘米.5.已知:如图△ABC中AB=AC,且EB=BD=DC=CF,∠A=40°,则∠EDF的度数为________.6.点O是平行四边形ABCD对角线的交点,若平行四边行ABCD的面积为8cm,则△AOB的面积为.7.如果圆的半径R增加10%,则圆的面积增加_________.8.梯形上底长为2,中位线长为5,则梯形的下底长为.9.△ABC三边长分别为3、4、5,与其相似的△A′B′C′的最大边长是10,则△A′B′C′的面积是.10.在Rt△ABC中,AD是斜边BC上的高,如果BC=a,∠B=30°,那么AD等于.练习二:选择题1.一个角的余角和它的补角互为补角,则这个角等于[]A.30°B.45°C.60°D.75°2.将一张矩形纸对折再对折(如图),然后沿着图中的虚线剪下,得到①、②两部分,将①展开后得到的平面图形是[]A.矩形B.三角形C.梯形D.菱形3.下列图形中,不是中心对称图形的是[]A.B.C.D.4.既是轴对称,又是中心对称的图形是[]A.等腰三角形B.等腰梯形C.平行四边形D.线段5.依次连结等腰梯形的各边中点所得的四边形是[]A.矩形B.正方形C.菱形D.梯形6.如果两个圆的半径分别为4cm和5cm,圆心距为1cm,那么这两个圆的位置关系是[]A.相交B.内切C.外切D.外离7.已知扇形的圆心角为120°,半径为3cm,那么扇形的面积为[]8.A.B.C三点在⊙O上的位置如图所示,若∠AOB=80°,则∠ACB等于[]A.160°B.80°C.40°D.20°9.已知:AB∥CD,EF∥CD,且∠ABC=20°,∠CFE=30°,则∠BCF的度数是[]A.160°B.150°C.70°D.50°(第9题图)(第10题图)10.如图OA=OB,点C在OA上,点D在OB上,OC=OD,AD和BC相交于E,图中全等三角形共有[]A.2对B.3对C.4对D.5对