【课件】162二次根式的乘除（第1课时二次根式的乘法）VIP免费

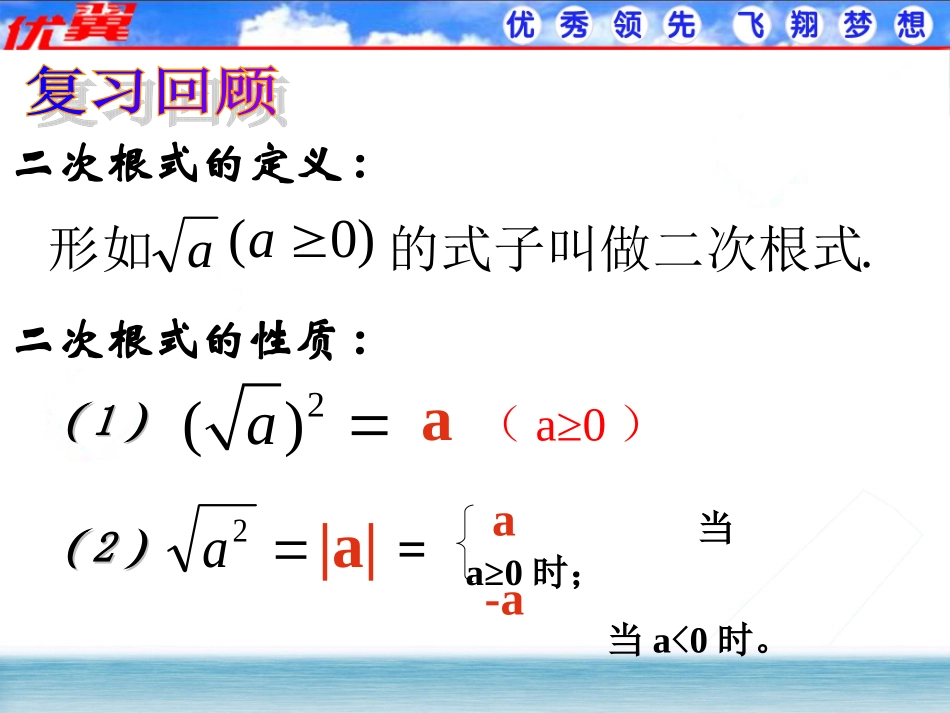
16.2二次根式的乘除第1课时二次根式的乘法.的式子叫做二次根式形如a)0(a二次根式的定义:（a≥0）2()a（（11））a-a|a|（（22））2aa二次根式的性质:当a≥0时；当a<0时。=动手试一试！•计算：.____________916___________916)2(.____________254___________254)1(；；100521441010341212思考：观察以上计算结果，你能发现什么？2×32×用你发现的规律填空25×3==能用字母表示你所发现的规律吗?2×5（1）二次根式乘法法则：一般地有0)b0,(ababa二次根式与二次根式相乘，等于各被开方数的积的算术平方根。注意：a、b必须为非负数baba注意：×例题1计算：（1）322（2）82124282128212.264322322.1解：8422)0(82aaaaa82)3(21682aaaa4（3）abba（a≥0，b≥0）二次根式的乘法：利用这个等式可以化简一些根式。在本章中，如果没有特别说明，所有的字母都表示正数．baab（a≥0，b≥0）反过来，就可得到积的算术平方根性质：例题２化简：（1）12（2）324ba)0,0(ba3223×43×43×解：12(1)2abb4bb×a22××ab432(2)?0,0)2(:呢的条件为若变≥ba≤化简二次根式的步骤：1.将被开方数尽可能分解出平方数.3.将平方项应用化简.aa2根式运算的结果中，被开方数应不含能开得尽方的因数或因式。2.应用baab（a≥0，b≥0）练习化简：322)6(,2)5(,9)4(50)3(,72)2(,24)1(baaa622625a32abab例题３计算：10253.2714.1.1xyx33.3.＝14×7＝7²×2.＝7²2＝72＝3×25×10＝65²×2＝65²×2230＝＝3x.1－3xy＝x²y＝xy2.化简:（1）（3）1.计算：y4121493216225cabxxy123527172128841232练习：（2）（4）（315）y（2）（6）（2）（2y）（77）（15）（4bcac）3.已知一个矩形的长和宽分别是，求这个矩形的面积。cm22cm10和）（254cmS10×222²×5210×225×2²210224、?9494对吗）（）（呢？）（）（怎样化简94×636)9()4(答：不对abba)0,0(ba非负数5：如图，在ABC中，∠C=90°,AC=10cm,BC=20cm.求：AB.ABC22BCACAB500201022)(5105105102cm答：AB长cm.510解:∵∠C=90°,根据勾股定理222BCACAB6：判断（1）4(x-y)=x-y4()（2）x²-y²=()x²y²-=x-y（3）1=1+=1494923+=123()×××1、本节课学习了积的算术平方根和算术平方根的积。abba)0,0(ba1.将被开方数尽可能分解出平方数.2、化简二次根式的步骤：2.应用baab（a≥0，b≥0）abba)0,0(ba3.将平方项应用化简.aa2