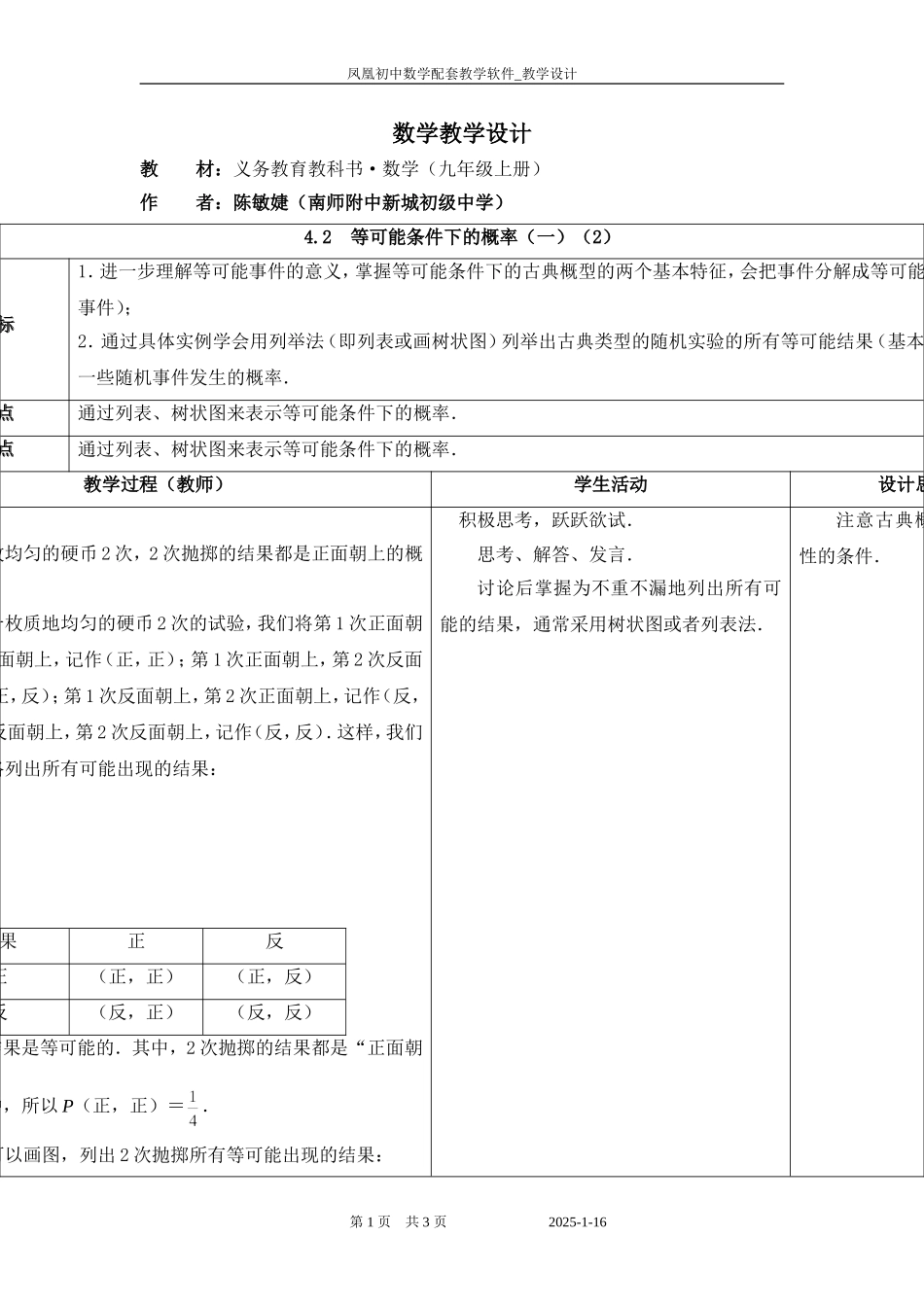
凤凰初中数学配套教学软件_教学设计数学教学设计教材:义务教育教科书·数学(九年级上册)作者:陈敏婕(南师附中新城初级中学)4.2等可能条件下的概率(一)(2)教学目标1.进一步理解等可能事件的意义,掌握等可能条件下的古典概型的两个基本特征,会把事件分解成等可能的结果(基本事件);2.通过具体实例学会用列举法(即列表或画树状图)列举出古典类型的随机实验的所有等可能结果(基本事件)并计算一些随机事件发生的概率.教学重点通过列表、树状图来表示等可能条件下的概率.教学难点通过列表、树状图来表示等可能条件下的概率.教学过程(教师)学生活动设计思路抛掷一枚均匀的硬币2次,2次抛掷的结果都是正面朝上的概抛掷一枚质地均匀的硬币2次的试验,我们将第1次正面朝次正面朝上,记作(正,正);第1次正面朝上,第2次反面朝上,记作(正,反);第1次反面朝上,第2次正面朝上,记作(反,次反面朝上,第2次反面朝上,记作(反,反).这样,我们可以利用表格列出所有可能出现的结果:结果正反正(正,正)(正,反)反(反,正)(反,反)种结果是等可能的.其中,2次抛掷的结果都是“正面朝种,所以P(正,正)=.我们还可以画图,列出2次抛掷所有等可能出现的结果:积极思考,跃跃欲试.思考、解答、发言.讨论后掌握为不重不漏地列出所有可能的结果,通常采用树状图或者列表法.注意古典概型中等可能性的条件.第1页共3页2025-1-16凤凰初中数学配套教学软件_教学设计像这样的图,我们称之为树状图,它可以帮助我们不重复、不遗漏地列出所有可能出现的结果.思考“先后两次掷一枚硬币”与“同时掷两枚硬币”,这两种试验的所有可能结果一样吗?同时掷两个质地均匀的骰子,计算下列事件的概率:)两个骰子的点数相同;)两个骰子点数的和是9;)至少有一个骰子的点数为2.如果把题中的“同时掷两个骰子”改为“把一个骰,所得到的结果有变化吗?1当一次试验要涉及两个因素(例如掷两个骰子)并且可能出现的结果数目较多时,为不重不漏地列出所有可能的结果,通常采用列表法.用树状图列举出结果,并感受到当一次试验要涉及3个或更多的步骤时,列表格就不方便了,通常采用树状图.当试验涉及两个因素(二维)时,可用列表的列举方法.结合表格,体会列表法对列举所有可能的结果所起的作用.当试验涉及三个因素(三维)时,列表法受限,自然过渡到用树形图的形式来列举.注意列表和树形图的适用条件,避免学生生搬硬套在情况少、类型少时,可直接作简单枚举.甲、乙、丙三只不透明的口袋中都装有1个白球、1个除颜色外都相同,搅匀后分别从三只口袋中任意摸出1从三只口袋摸出的都是红球的概率是多少?此时,列表能否列举出所有可能的结果?2当一次试验要涉及3个或更多的因素(例如从三只口)时,列表就不方便了,为了不重不漏地列出所有可能的结果,通常采用树形图.当事件要经过多次步骤(三步以上)完成“树形图”的方法求事件的概率很有效.列举法有哪些?列表与画树状图分别有哪些适用条件?)若从三只口袋摸出的球中有一只白球、两只红球的概率是第2页共3页2025-1-16凤凰初中数学配套教学软件_教学设计一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从袋中任意摸出1个球,记录颜色后放摇匀,再从中任意摸出1个球.求两次摸到红球颜色的概率.北京2008年奥运会吉祥物“福娃”是“贝贝、晶晶、欢欢、迎迎、妮妮”:张分别印有5个“福娃”图案的卡片(卡片的形状、大小、质地都相同)放在盒子中,搅匀后从中取出1张卡片,记录后放回、搅匀,再从中取出1张卡片.求下列事件的发生的概率:)取出的2张卡片相同;)取出的2张卡片中,1张为“欢欢”,1张为“贝贝”;)取出的2张卡片中,至少有1张为“欢欢”.交流、讨论.用“树状图”或“表格”列出所有可能出现的结果.例1把2个红球编号为红球1、红球2.例2可将印有“贝贝、晶晶、欢欢、迎迎、妮妮”的卡片分别编号为1、2、3、4、5.突出等可能条件下概率(一)(即古典概型)的两个基本特征——试验结果的有限性和等可能性.论”计算概率的格式例1中为区分可以把2个红球编号为红球1、...