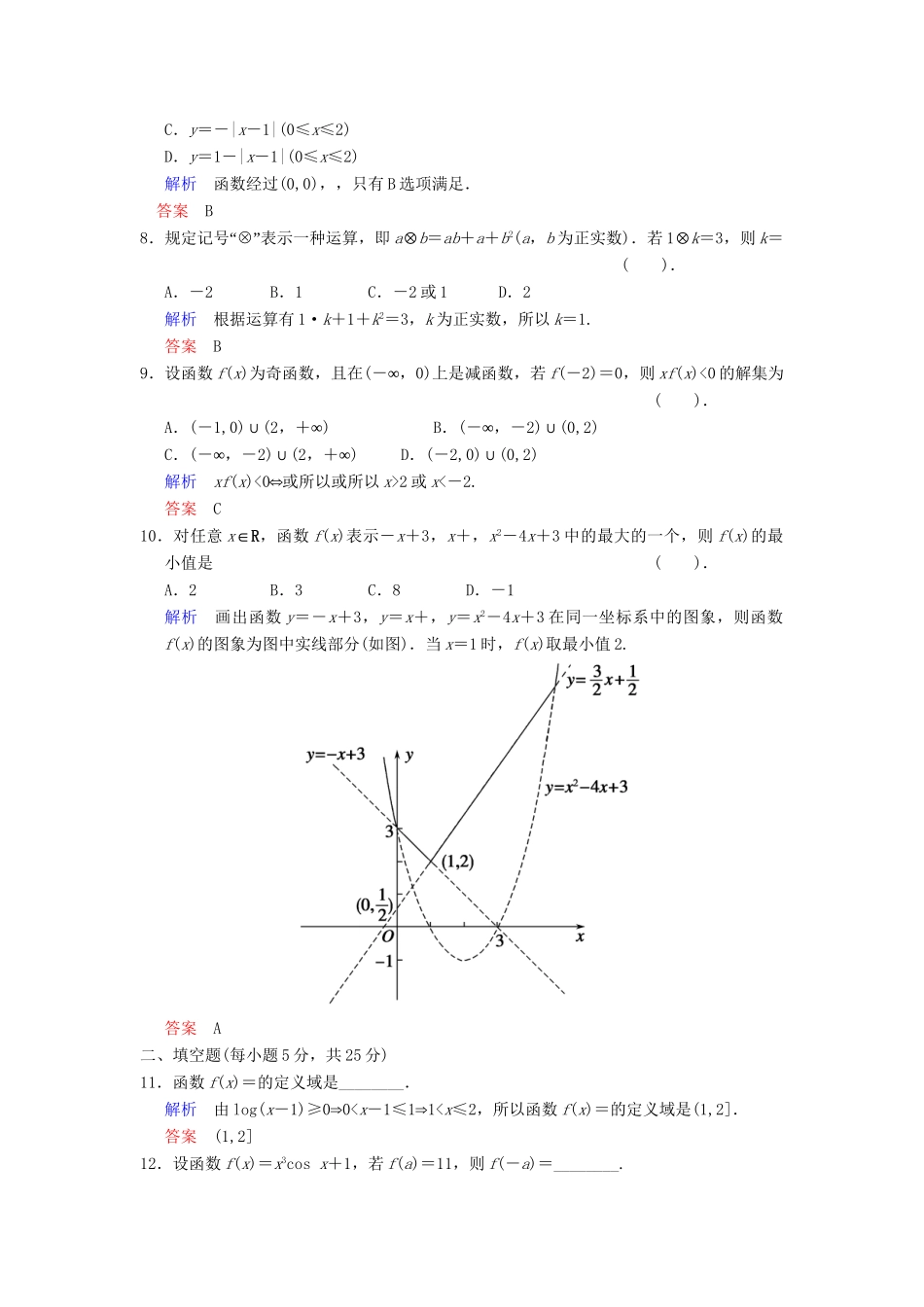
小题专项集训(二)函数的概念、图象和性质(时间:40分钟满分:75分)一、选择题(每小题5分,共50分)1.函数y=的值域是().A.[0∞,+)B.[0,4]C.[0,4)D.(0,4)解析∵4x>0,∴0≤16-4x<16,∴∈[0,4).答案C2.设f(x)是R上的任意函数,则下列叙述正确的是().A.f(x)f(-x)是奇函数B.是奇函数C.f(x)-f(-x)是偶函数D.f(x)+f(-x)是偶函数解析F(x)=f(x)+f(-x)=f(-x)+f(x)=F(-x).答案D3.若f(x)是R上周期为5的奇函数,且满足f(1)=1,f(2)=2,则f(3)-f(4)=().A.-1B.1C.-2D.2解析f(3)-f(4)=f(-2)-f(-1)=-f(2)+f(1)=-2+1=-1.答案A4.已知函数f(x)=若f(a)=,则a的值为().A.-1B.C.-1或D.-1或解析若a>0,有log2a=,a=;若a≤0,有2a=,a=-1.答案D5.函数y=f(x)在R上单调递增,且f(m2+1)>f(-m+1),则实数m的取值范围是().A.(∞-,-1)B.(0∞,+)C.(-1,0)D.(∞-,-1)∪(0∞,+)解析由题意得m2+1>-m+1,即m2+m>0,故m<-1或m>0.答案D6.奇函数f(x)在[3,6]上是增函数,且在[3,6]上的最大值为2,最小值为-1,则2f(-6)+f(-3)=().A.5B.-5C.3D.-3解析由题意又∵f(x)是奇函数,∴2f(-6)+f(-3)=-2f(6)-f(3)=-4+1=-3.答案D7.图中的图象所表示的函数解析式为().A.y=|x-1|(0≤x≤2)B.y=-|x-1|(0≤x≤2)C.y=-|x-1|(0≤x≤2)D.y=1-|x-1|(0≤x≤2)解析函数经过(0,0),,只有B选项满足.答案B8“.规定记号⊗”表示一种运算,即a⊗b=ab+a+b2(a,b为正实数).若1⊗k=3,则k=().A.-2B.1C.-2或1D.2解析根据运算有1·k+1+k2=3,k为正实数,所以k=1.答案B9.设函数f(x)为奇函数,且在(∞-,0)上是减函数,若f(-2)=0,则xf(x)<0的解集为().A.(-1,0)∪(2∞,+)B.(∞-,-2)∪(0,2)C.(∞-,-2)∪(2∞,+)D.(-2,0)∪(0,2)解析xf(x)<0⇔或所以或所以x>2或x<-2.答案C10.对任意x∈R,函数f(x)表示-x+3,x+,x2-4x+3中的最大的一个,则f(x)的最小值是().A.2B.3C.8D.-1解析画出函数y=-x+3,y=x+,y=x2-4x+3在同一坐标系中的图象,则函数f(x)的图象为图中实线部分(如图).当x=1时,f(x)取最小值2.答案A二、填空题(每小题5分,共25分)11.函数f(x)=的定义域是________.解析由log(x-1)≥0⇒0f(x2),则f(x)是减函数;③若f(x)是定义在R上的奇函数,且f(x+2)也为奇函数,则f(x)是以4为周期的周期函数.其中真命题的序号是________.解析对于①,由f(x)+f(2-x)=0知,其图象关于点(1,0)对称.又因为f(x)是定义域为R的奇函数,所以f(2-x)=-f(x)=f(-x),故该函数周期为2,①错误;对于②,不符合减函数的定义,②错误;对于③,由题意知,f(x+2)=-f(-x+2)=f(x-2),故周期为4,③正确.所以真命题的序号为③.答案③