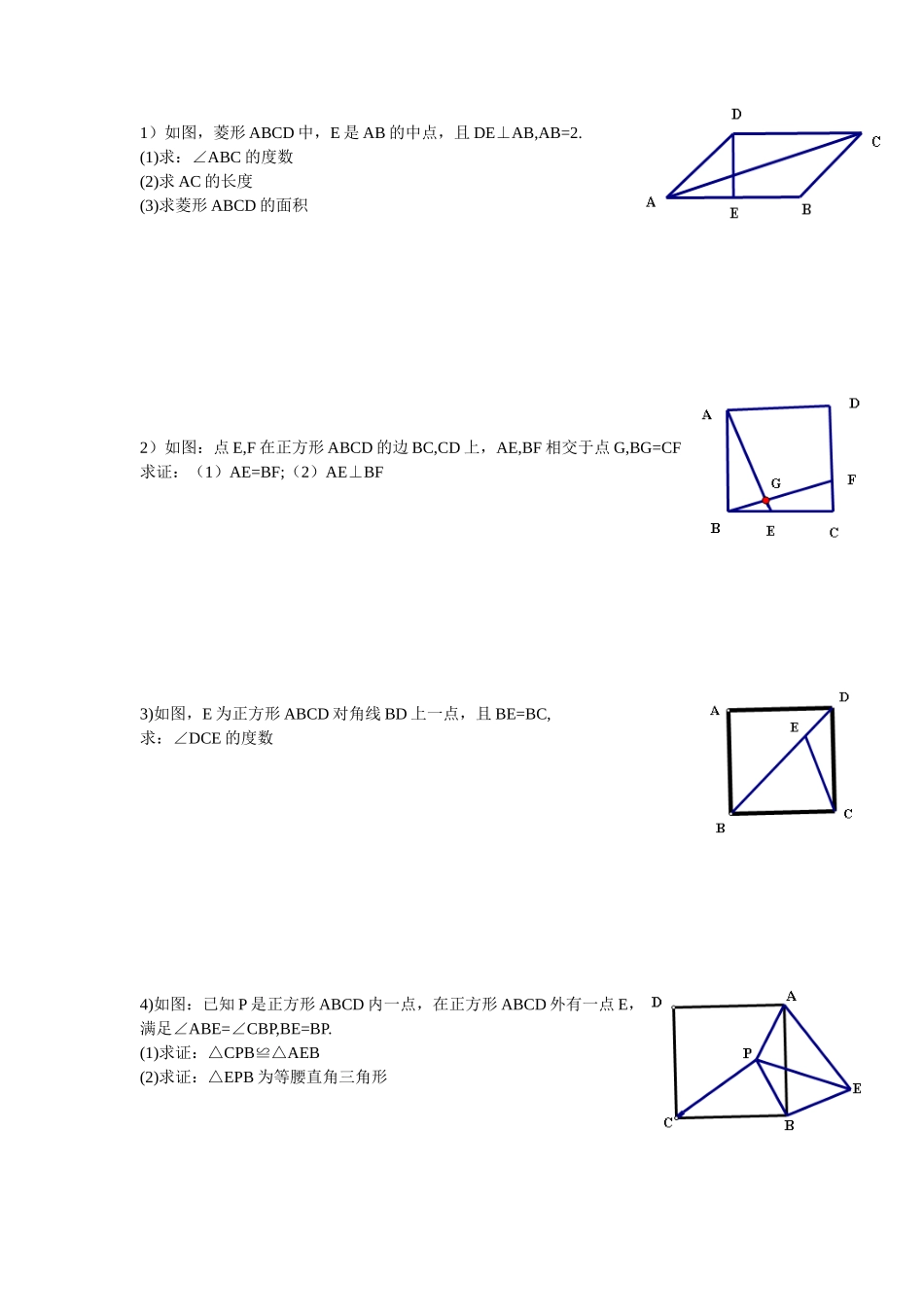
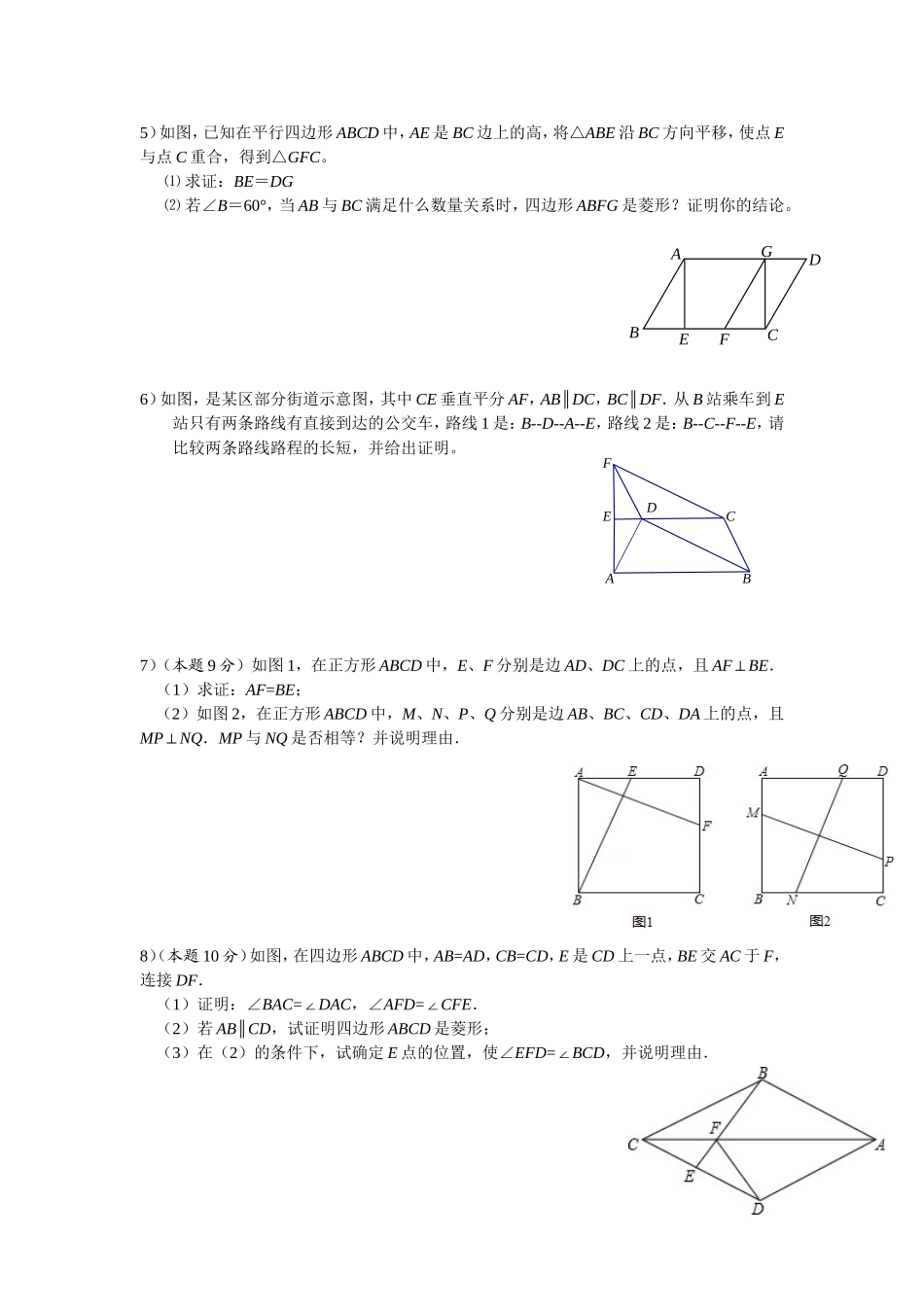
1)如图,菱形ABCD中,E是AB的中点,且DE⊥AB,AB=2.(1)求:∠ABC的度数(2)求AC的长度(3)求菱形ABCD的面积2)如图:点E,F在正方形ABCD的边BC,CD上,AE,BF相交于点G,BG=CF求证:(1)AE=BF;(2)AE⊥BF3)如图,E为正方形ABCD对角线BD上一点,且BE=BC,求:∠DCE的度数4)如图:已知P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.(1)求证:△CPB≌△AEB(2)求证:△EPB为等腰直角三角形5)如图,已知在平行四边形ABCD中,AE是BC边上的高,将△ABE沿BC方向平移,使点E与点C重合,得到△GFC。⑴求证:BE=DG⑵若∠B=60°,当AB与BC满足什么数量关系时,四边形ABFG是菱形?证明你的结论。6)如图,是某区部分街道示意图,其中CE垂直平分AF,AB∥DC,BC∥DF.从B站乘车到E站只有两条路线有直接到达的公交车,路线1是:B--D--A--E,路线2是:B--C--F--E,请比较两条路线路程的长短,并给出证明。7)(本题9分)如图1,在正方形ABCD中,E、F分别是边AD、DC上的点,且AF⊥BE.(1)求证:AF=BE;(2)如图2,在正方形ABCD中,M、N、P、Q分别是边AB、BC、CD、DA上的点,且MP⊥NQ.MP与NQ是否相等?并说明理由.8)(本题10分)如图,在四边形ABCD中,AB=AD,CB=CD,E是CD上一点,BE交AC于F,连接DF.(1)证明:∠BAC=∠DAC,∠AFD=∠CFE.(2)若AB∥CD,试证明四边形ABCD是菱形;(3)在(2)的条件下,试确定E点的位置,使∠EFD=∠BCD,并说明理由.ADGCBFEBECDFA