圆锥曲线定义应用VIP免费

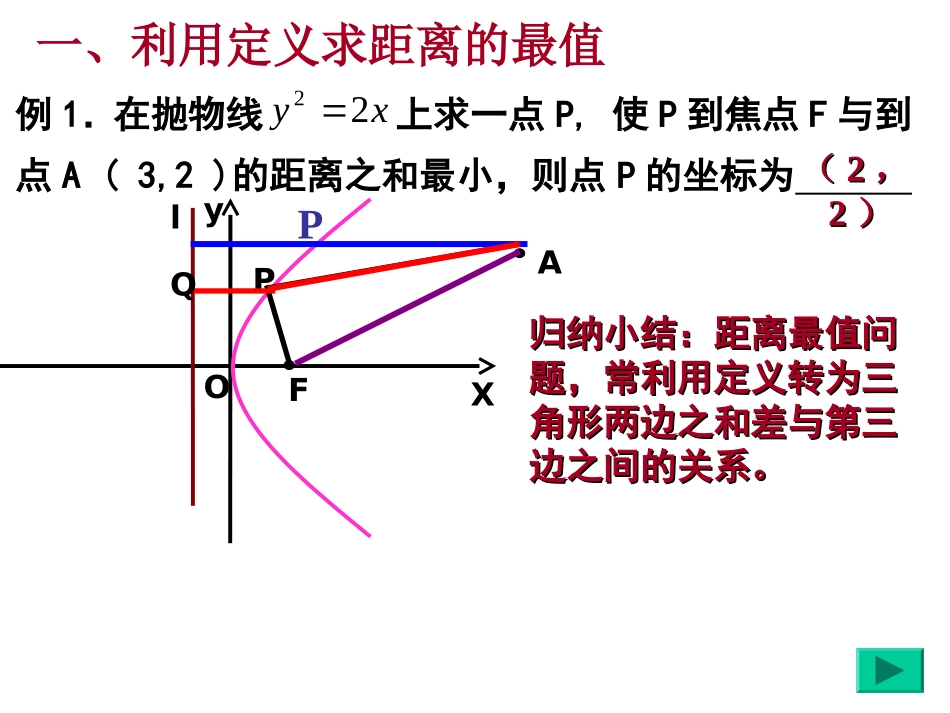
圆锥曲线定义的应用（二）圆锥曲线定义的应用（二）（理科）（理科）邕宁高中高三数学备课组邕宁高中高三数学备课组定义回顾：定义回顾：椭圆的定义：椭圆的定义：点集点集M={P||PFM={P||PF11|+|PF|+|PF22|=2a|=2a，，2a2a＞＞|F|F11FF22|}|}的点的轨迹。的点的轨迹。双曲线的定义：双曲线的定义：点集点集M={P|M={P|︱︱|PF|PF11|-|PF|-|PF22||︱︱=2a=2a，，}}的点的轨迹。的点的轨迹。|)|2(21FFa抛物线的定义：抛物线的定义：到一个定点Ｆ的距离与到一条得直到一个定点Ｆ的距离与到一条得直线Ｌ的距离相等的点的轨迹。线Ｌ的距离相等的点的轨迹。统一定义：统一定义：M={P|M={P|，，}0}0＜＜ee＜＜11为椭圆，为椭圆，e>1e>1为双曲线，为双曲线，ee＝＝11为抛物线。为抛物线。edPF例1．在抛物线xy22上求一点P,使P到焦点F与到点A(3,2)的距离之和最小，则点P的坐标为AXyOFPlP（（22，，22））一、利用定义求距离的最值Q归纳小结：距离最值问归纳小结：距离最值问题，常利用定义转为三题，常利用定义转为三角形两边之和差与第三角形两边之和差与第三边之间的关系。边之间的关系。高考再现一:（08辽宁）已知点P是抛物线y2=2x上的一个动点，则点P到点M（0，2）的距离与点P到该抛物线准线的距离之和的最小值（）A.B.3C.D.217529Ay轴OFPyMXlP高考再现二:(09四川理)已知直线和直线，抛物线上一动点P到直线和直线的距离之和的最小值是()A.2B.3C.D.AXyOFQ2l1lPM1:4360lxy2:1lx24yx1l2l5111637NP高考命题规律：（1）一个动点到两个定点（其中一个为焦点）的距离之和的最值；（2）一个动点到一个定点和到一条定直线（准线）的距离之和的最值；（3）一个动点到两条定直线（其中一条为准线）的距离之和的最值；2.2.思想方法：思想方法：等价转换思想，数形结合思想等价转换思想，数形结合思想方法归纳小结：1.解题思路：注意灵活运用抛物线上的点到焦点的距离与到准线距离的等价转化，“看到准线想焦点,看到焦点想准线”。例2.已知点，F是椭圆的左焦点，一动点M在椭圆上移动，则|AM|+2|MF|的最小值为_____1121622yx32，A方法归纳：注意方法归纳：注意22是，是，必须用统一定义来进行转换，必须用统一定义来进行转换，双曲线也类似方法。双曲线也类似方法。e1类比应用1——椭圆.A.F.MMXYO10提示：由统一定义得2|MF|=ddN变式一、已知，，是椭圆的左右焦点，M是椭圆上的一点。（1）求的范围（2）求的最小值225945xy(1,1)A1F2F2MAMF132MFMAAF1F2MYOX(2)11MM归纳总结：一定化为，其中为MFnMAm)MFmnMAm（mne1变式二:已知椭圆上一动点P到直线和直线的距离分别为d1,d2，则d1+d2之和的最小值是()A.5B.3C.2D.XYF1F21l2lPd1d2o225945xy02434:1yxl29:2xl32532DMPN提示：由统一定义得：d2=｜PF2|322.2.思想方法：思想方法：等价转换思想，数形结合思想等价转换思想，数形结合思想(1)(1)涉及圆锥曲线上的点与两个焦点问题，常用涉及圆锥曲线上的点与两个焦点问题，常用第一定义。第一定义。(2)(2)涉及圆锥曲线上的点与焦点、准线问题，常用涉及圆锥曲线上的点与焦点、准线问题，常用统一的定义。统一的定义。方法归纳小结：1.解题思路：(3)注意观察结构式系数特点选择定义进行等价转化。若与离心率有关，则用统一定义；否则可能用第一定义。xyA.FOMM例例33、已知Ａ（，３）为一定点，Ｆ为双曲、已知Ａ（，３）为一定点，Ｆ为双曲线的右焦点，Ｍ在双曲线右支上移线的右焦点，Ｍ在双曲线右支上移动，当动，当||ＡＭＡＭ||＋＋||ＭＦＭＦ||最小时，求Ｍ点最小时，求Ｍ点的坐标．的坐标．211127922yx21类比应用2——双曲线答案：），（332MN变式一:已知F是双曲线的左焦点，定点A（1，4），P是双曲线右支上的动点，则的最小值为____.221412yx||||PFPA9FOAPxyF2P变式二:已知双曲线右支上一动点P到直线和直线的距离分别为d1,d2，则d1+2d2之和的最小值是()A.5B.3C.2D.221412yx012:1yxl1:2xl559OFPxyd1d2DPM例4.已知分别是双曲线的两个焦点，A和B是以O(O为坐标原点)为圆心，为半径的圆与该双曲线左支的两个交点,且是等边三角形，则双曲线的离...