三角函数的图像和性质1VIP免费

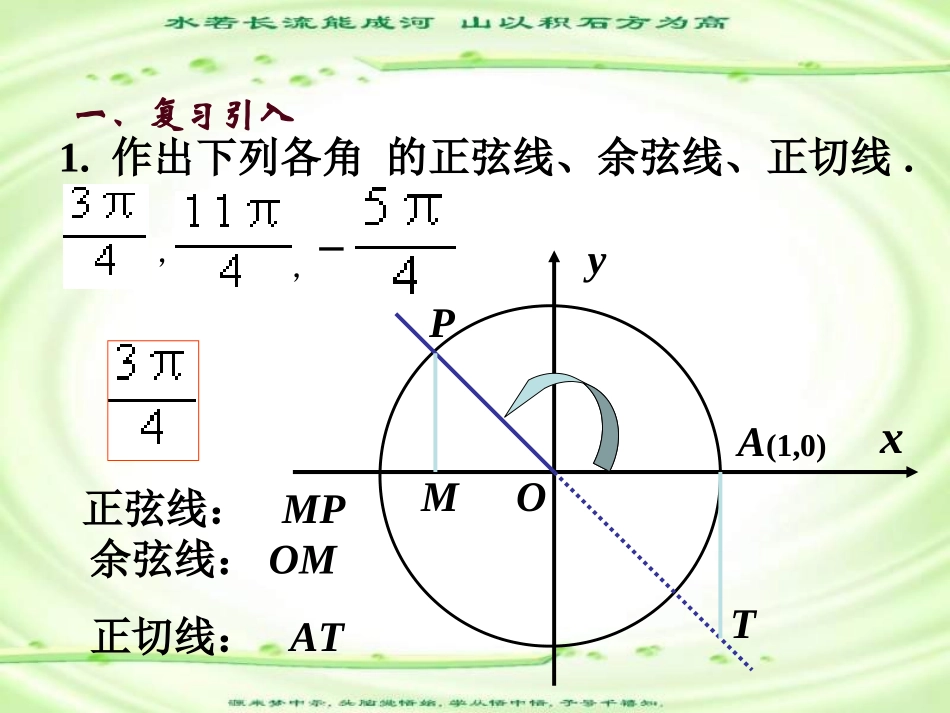
三角函数的图像与性质（一）主讲：李光遥奎屯王新敞新疆教学目的：教学重点：教学难点：1.掌握五点作图法的三个步骤，即：列表、描点、连线；2.掌握函数图象的变换过程。1.五点法做函数图象及有关问题；2.函数图象变换问题。采用不同的方法对函数图象进行变换。一、复习引入1.作出下列各角的正弦线、余弦线、正切线._，，xyPOA(1,0)T正弦线：MP余弦线：OM正切线：ATM一、复习引入1.作出下列各角的正弦线、余弦线、正切线.xyPOA(1,0)T正弦线：MP余弦线：OM正切线：ATM_，，一、复习引入1.作出下列各角的正弦线、余弦线、正切线.xyPOA(1,0)T正弦线：MP余弦线：OM正切线：ATM__，，一、复习引入2.讨论的正弦线、余弦线、正切、线的情况.xyoPMA(1,0)正弦线：MP余弦线变为一个点正切线不存在一、复习引入xyoPMA(1,0)T正弦线变为一个点余弦线：OM正切线变为一个点2.讨论的正弦线、余弦线、正切线的情况.、函数2,0,sinxxy图象的几何作法....利用三角函数线作三角函数图象作三角函数线得三角函数值，描点)sin,(xx,连线作如:3x3的正弦线,MP平移定点),(MPx几何法作图的关键是如何利用单位圆中角x的正弦线，巧妙地移动到直角坐标系内，从而确定对应的点(x,sinx).二、重难点讲解1.作正弦函数的图象：xyo1-12AB(B)(O1)O1y=sinx,x[0,2]二、重难点讲解作正弦函数的图象xyoABO1y=sinx,x[0,2]2-1-11再演示一遍……作正弦函数的图象xyoABO1y=sinx,x[0,2]2-1-11再演示一遍……作正弦函数的图象xyoABO1y=sinx,x[0,2]2-1-11再演示一遍……作正弦函数的图象xyoABO1y=sinx,x[0,2]2-1-11再演示一遍……作正弦函数的图象xyoABO1y=sinx,x[0,2]2-1-11再演示一遍……作正弦函数的图象xyoABO1y=sinx,x[0,2]2-1-11再演示一遍……作正弦函数的图象xyoABO1y=sinx,x[0,2]2-1-11再演示一遍……作正弦函数的图象xyoABO1y=sinx,x[0,2]2-1-11再演示一遍……作正弦函数的图象：xyoABO1y=sinx,x[0,2]2-1-11二、重难点讲解2.正弦曲线：xyo1-1-2-234y=sinx,xR二、重难点讲解二、重难点讲解余弦曲线y------1-12o46246)cos(cosxxy)2sin()](2sin[xx由于所以余弦函数Rxxy,cos与函数Rxxy),2sin(是同一个函数；2余弦函数的图像可以通过正弦曲线向左平移个单位长度而得到．y=cosx,xR∈3.余弦函数图象的作法y=sinx,xR∈余弦曲线的几何作法4.正弦函数、余弦函数的图象：xy0yx0-11-1124624624246y=sinx,xR∈y=cosx,xR∈正弦曲线余弦曲线二、重难点讲解简图作法：(五点作图法)与x轴的交点)0,0()0,()0,2(图象的最高点图象的最低点)1,(23与x轴的交点)0,(2)0,(23图象的最高点)1,0()1,2(图象的最低点)1,()1,2((1)列表(列出对图象形状起关键作用的五点坐标)(3)连线(用光滑的曲线顺次连结五个点)(2)描点(定出五个关键点)oxy---11-32326567342335611262oxy---11-32326567342335611265.五点作图法的五个关键点二、重难点讲解三、例题讲解（2）列表例1画出下列函数的简图（1）y=sinx+1,x∈[0,2π];列表描点作图xxsin1sinx101010210102232（2）y=-cosx,x∈[0,2π].解:（1）]2,0[,sin1xxy]2,0[,sinxxyxxcosxcos02232211yo223x10-101-1010-1]2,0[,cosxxy]2,0[,cosxxy2223211xyo三、例题讲解例2画出函数y=1-sinx,x[0,2π]∈的简图.列表描点作图xxsin1sinx101010012102232解法一:（五点法作图）1sin,[0,2]yxx]2,0[,sinxxy2223211xyo解法二:（变换法作图）①先作出函数y=sinx的图像；②其次将函数y=sinx的图像关于x轴对称得到y=-sinx的图像；③最后将函数y=-sinx的图像整体向上平移1个单位就是y=1-sinx的图像.四、练习(1)作函数y=1+3cosx，x[0,2π]∈的简图(2)作函数y=2sinx-1，x[0,2π]∈的简图解：(1)解：(2)y0xΠΠ/23Π/22Π-3213-1-2y0xΠ/2Π3Π/22Π-23-1241五、...