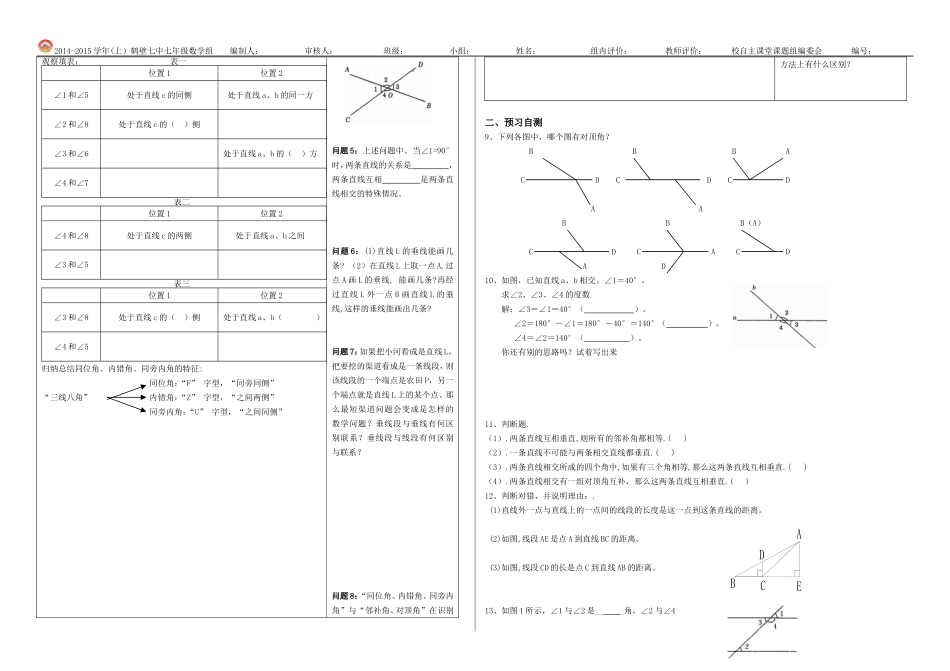
abc2014-2015学年(上)鹤壁七中七年级数学组编制人:审核人:班级:小组:姓名:组内评价:教师评价:校自主课堂课题组编委会编号:§5.1相交线【使用说明及学法指导】1.先精读一遍教材(P160—P167),用红色笔进行勾画;再针对预习自学二次阅读并回答;2.若预习完可对合作探究部分认真审题,做不完的正课时再做;3.找出自己的疑惑和需要讨论的问题准备课上讨论质疑。4.预习指导:认真学习对顶角、邻补角、垂直、垂线段及点到直线的距离的概念,掌握对顶角的性质,垂线的基本事实,能识别三种角。【学习目标】1.了解两条直线相交所构成的角,理解并掌握对顶角、邻补角的概念和性质,并会用这个性质进行简单的计算。2、了解垂直概念,能说出垂线的性质,会用三角尺或量角器过一点画一条直线的垂线。3、了解垂线段的概念,了解垂线段最短的性质,体会点到直线的距离的意义,并会度量点到直线的距离。4、理解同位角、内错角、同旁内角的意义,会熟练地识别图中的同位角、内错角、同旁内角。5、培养学生分析、抽象、归纳能力,培养学生的识图能力自学案一、预习自学:基础知识梳理问题导引1、①任意画两条相交直线,在形成的四个角(∠1,∠2,∠3,∠4)中,两两相配共能组成对角,分别是。②分别测量一下各个角的度数,是否发现规律?你能否把他们分类?完成教材P160的表格。③再画两条相交直线比较。.2、归纳:邻补角、对顶角定义两条直线相交所构成的四个角中,有公共顶点的两个角是邻补角。两条直线相交所构成的四个角中,有公共顶点的两个角是对顶角。3、邻补角的性质:邻补角。问题1:观察思考:剪刀剪开纸张的过程,随着两个把手之间的角逐渐变小,剪刀刃之间的角度也相应。我们把剪刀的构成抽象为两条直线,就是我们要研究的两条相交直线所成的角的问题。问题2:①两条直线相交所构成的四个角中,邻补角有对,对顶角有对。②对顶角形成的前提条件是。问题3:邻补角是互补的一种特殊的情况,其数量关系是?位置关系为?问题4:完成以下推理过程:如图, ∠1+∠2=4、由推理可知,对顶角的性质:对顶角。5、用语言概括垂直定义:两条直线相交,所成四个角中有一个角是时,我们称这两条直线,其中一条直线是另一条的,它们的交点叫做。垂直的表示方法:如果直线AB、CD互相垂直,记作,垂足为O。6、①用三角尺或量角器画已知直线L的垂线.L②你能得出什么结论?7、画图验证:(1)画直线L,在L外取一点P;(2)过P点出PO⊥L,垂足为O;(3)点A1,A2,A3……在L上,连接PA、PA2、PA3……;(4)用度量法比较线段PO、PA1、PA2、PA3……的大小,.得出线段最小。①归纳结论:连接直线外一点与直线上各点的所有线段中,。简单说成:.②线段PO、PA1、PA2、PA3、PA4……中,哪一条或几条线段的长度是点P到直线L的距离?即叫做点到直线的距离8、如图,直线c分别与直线a、b相交(也可以说两条直线a、b被第三条直线c所截),得到8个角,通常称为“三线八角”,那么这8个角之间有哪些关系呢?,∠2+∠3=。(邻补角定义)∴∠1=180°-,∠3=180°-(等式性质)∴∠1=∠3(等量代换)EDCBA2014-2015学年(上)鹤壁七中七年级数学组编制人:审核人:班级:小组:姓名:组内评价:教师评价:校自主课堂课题组编委会编号:观察填表:表一位置1位置2∠1和∠5处于直线c的同侧处于直线a、b的同一方∠2和∠8处于直线c的()侧∠3和∠6处于直线a、b的()方∠4和∠7表二位置1位置2∠4和∠8处于直线c的两侧处于直线a、b之间∠3和∠5表三位置1位置2∠3和∠8处于直线c的()侧处于直线a、b()∠4和∠5归纳总结同位角、内错角、同旁内角的特征:同位角:“F”字型,“同旁同侧”“三线八角”内错角:“Z”字型,“之间两侧”同旁内角:“U”字型,“之间同侧”问题5:上述问题中、当∠1=90°时,两条直线的关系是,两条直线互相是两条直线相交的特殊情况。问题6:(1)直线L的垂线能画几条?(2)在直线L上取一点A,过点A画L的垂线,能画几条?再经过直线L外一点B画直线L的垂线,这样的垂线能画出几条?问题7:如果把小河看成是直线L,把要挖的渠道看成是一条线段,则该线段的一个端点是农田P,另一个端点就是直线L上的某个点。那么最短渠...