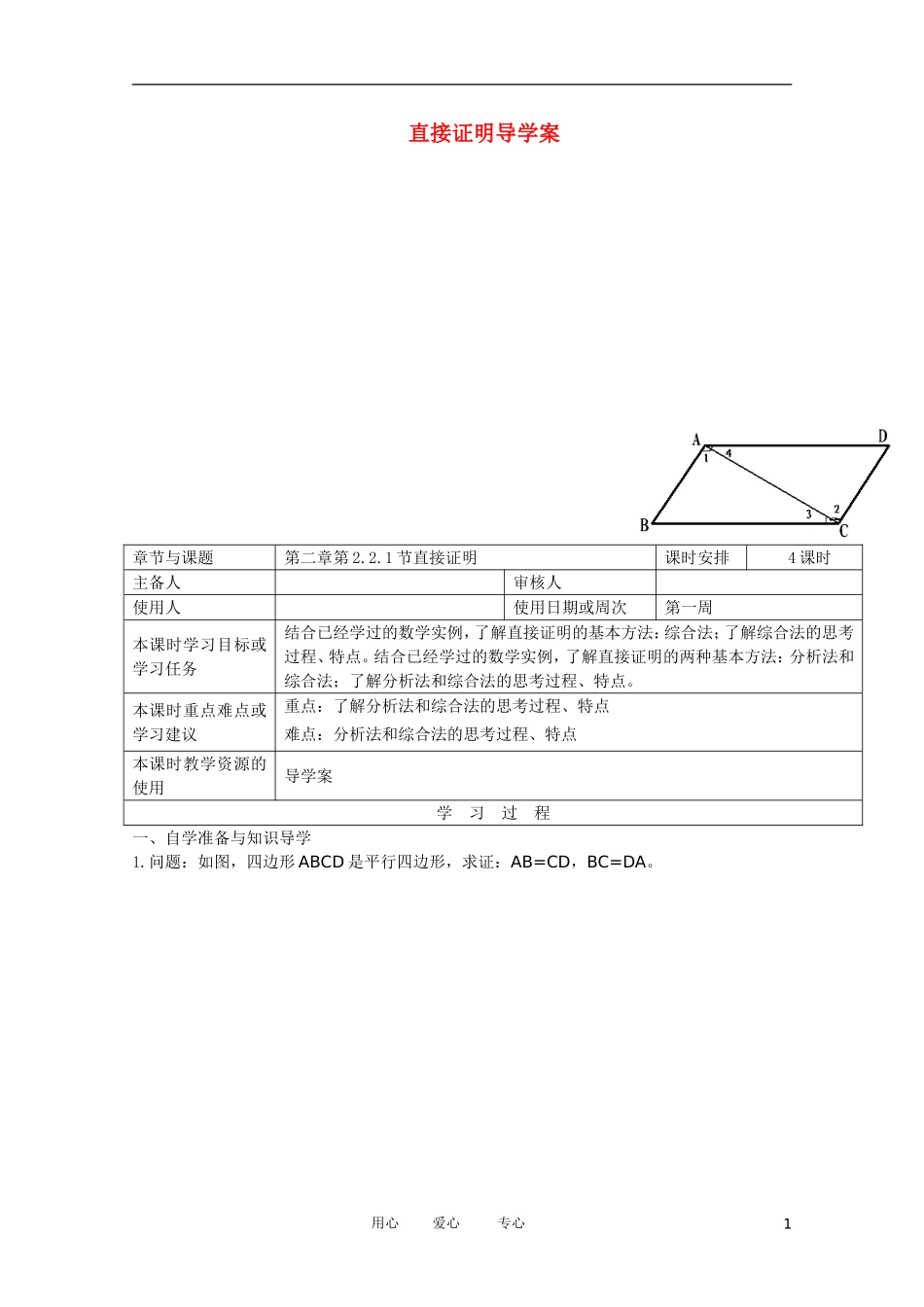
直接证明导学案章节与课题第二章第2.2.1节直接证明课时安排4课时主备人审核人使用人使用日期或周次第一周本课时学习目标或学习任务结合已经学过的数学实例,了解直接证明的基本方法:综合法;了解综合法的思考过程、特点。结合已经学过的数学实例,了解直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程、特点。本课时重点难点或学习建议重点:了解分析法和综合法的思考过程、特点难点:分析法和综合法的思考过程、特点本课时教学资源的使用导学案学习过程一、自学准备与知识导学1.问题:如图,四边形ABCD是平行四边形,求证:AB=CD,BC=DA。用心爱心专心1即需证(a-b)2>0成立。而由已知条件可知,a≠b,有a-b≠0,所以(a-b)2>0显然成立,由此命题得证。思考:以上证明方法有什么特点?__________________________。3.直接证明定义:直接从逐步推得成立的,这种证明通常称为直接证明.常用的直接证明方法有综合法与分析法.(1)综合法与分析法要点解析表综合法分析法定义思维过程思维特点步骤(2)对分析法证题的说明“若A成立,则B成立”,此命题用分析法证明的步骤如下:注:①②③(3)综合法和分析法的优缺点二、学习交流与问题探讨例1.已知:AB,CD相交于点O,△ACD≌△BDO,AE=BF.求证:CE=DF(分别用综合法和分析法证明)例2.求证:例3已知a>0,b>0,求证a(b2+c2)+b(c2+a2)≥4abc例4.已知abc,求证:1140abbcca≥.用心爱心专心2例5若a,b,c是不全相等的正数,求证:lglglglglglg222abbccaabc.三、练习检测与拓展延伸课本P81练习1、2、3、4练习:1.,求证:2.△ABC三边长a,b,c的倒数成等差数列,求证:∠B<900四、课后反思用心爱心专心3